색인 (Index)
색인 (Index)
- 벡터 및 스칼라 필드에 대한 검색 속도를 높이기 위한 구조.
- 한 필드에 대해 하나의 인덱스를 생성할 수 있다.
- 필드의 데이터 타입에 따라 적용할 수 있는 인덱스의 종류가 다르다.
- 장점 : 벡터 검색과 스칼라 필터링 성능(속도) 향상
- 단점 : 전처리 작업 필요, 메모리를 추가 사용
데이터타입 별 적용 가능한 인덱스
| 필드 데이터 유형 | 적용 가능한 인덱스 유형 |
|---|---|
| FLOAT - FLOAT_VECTOR - FLOAT16_VECTOR - BFLOAT16_VECTOR |
- FLAT - IVF_FLAT - IVF_SQ8 - IVF_PQ - GPU_IVF_FLAT - GPU_IVF_PQ - HNSW - DISKANN |
| BINARY_VECTOR | - BIN_FLAT - BIN_IVF_FLAT |
| SPARSE_FLOAT_VECTOR | - SPARSE_INVERTED_INDEX |
| VARCHAR | - INVERTED(권장) - BITMAP - Trie |
| BOOL | - BITMAP(권장) - INVERTED |
| INT - INT8 - INT16 - INT32 - INT64 |
- INVERTED - STL_SORT |
| FLOAT DOUBLE |
- INVERTED |
| ARRAY - BOOL - INT - VARCHAR |
- BITMAP(권장) |
| ARRAY - BOOL - INT~ - FLOAT~ - DOUBLE - VARCHAR |
- INVERTED |
| JSON | - INVERTED |
Scalar Index
스칼라 인덱싱 유형
| 스칼라 인덱싱 유형 | 설명 |
|---|---|
| 자동 인덱싱 | - 필드의 데이터 유형에 따라 Milvus가 인덱스 유형을 자동으로 결정. - 특정 인덱스 유형을 제어할 필요가 없는 경우에 적합. |
| 사용자 지정 인덱싱 | - 반전 인덱스 또는 비트맵 인덱스와 같은 정확한 인덱스 유형을 지정. - 이렇게 하면 인덱스 유형 선택을 더 세밀하게 제어 가능. |
파라미터
add_index(): 인덱스 파라미터 set에 인덱스 추가
| 파라미터 | 설명 | 예시 |
|---|---|---|
| field_name | 인덱싱할 스칼라 필드의 이름 | field_name=’title’ |
| index_type | 생성할 인덱스의 유형. (비우면 자동 지정) | index_type=’INVERTED’ |
| index_name | 생성할 인덱스의 이름. | index_name=’idx_title’ |
create_index(): 인덱스 파라미터를 토대로 인덱스 생성
| 파라미터 | 설명 | 예시 |
|---|---|---|
| collection_name | 인덱스가 생성될 컬렉션의 이름 | collection_name=’c1’ |
| index_params | 인덱스 구성을 포함하는 IndexParams 객체 | index_params=index_params |
자동 인덱싱
- 필드의 데이터 유형에 따라 Milvus가 인덱스 유형을 자동으로 결정.
- 특정 인덱스 유형을 제어할 필요가 없는 경우에 적합.
add_index()메서드에인덱스 유형 파라미터를 생략하면 됨.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Auto indexing
client = MilvusClient(
uri="http://localhost:19530"
)
index_params = MilvusClient.prepare_index_params()
index_params.add_index(
field_name="scalar_1",
index_type="", # auto indexing
index_name="default_index" # Name of the index to be created
)
client.create_index(
collection_name="test_scalar_index", # Specify the collection name
index_params=index_params
)
사용자 정의 인덱싱
- 정확한 인덱스 유형을 지정.
- 인덱스 유형 선택을 더 세밀하게 제어 가능.
add_index()메서드에index_type을 명시하면 됨.
1
2
3
4
5
6
7
8
9
10
11
12
index_params = MilvusClient.prepare_index_params()
index_params.add_index(
field_name="scalar_2",
index_type="INVERTED", # Type of index to be created
index_name="inverted_index" # Name of the index to be created
)
client.create_index(
collection_name="test_scalar_index", # Specify the collection name
index_params=index_params
)
- 사용자 지정 인덱싱
index_type목록
| index_type | 설명 |
|---|---|
| INVERTED | - 권장 - IVT는 텍스트에서 추출한 토큰을 알파벳순으로 정렬하여 저장 |
| BITMAP | - 필드에 있는 모든 고유 값의 비트맵을 저장하는 인덱스 유형 |
| STL_SORT | - 표준 템플릿 라이브러리 정렬 알고리즘을 사용해 스칼라 필드를 정렬 - 숫자 유형의 필드만 지원 |
| Trie | - 빠른 접두사 검색 및 검색을 위한 트리 데이터 구조 - VARCHAR 필드를 지원 |
참고
id필드는 기본적으로 인덱싱이 되기 때문에 별도 인덱싱 필요 없음.
Vector Index
파라미터
| 파라미터 | 설명 | 예시 |
|---|---|---|
| field_name | 인덱싱할 스칼라 필드의 이름 | field_name=’my_vector’ |
| index_type | 생성할 인덱스의 유형. (비우면 자동 지정) | index_type=’IVF_FLAT’ |
| index_name | 생성할 인덱스의 이름. | index_name=’idx_vector’ |
| metric_type | 벡터간 거리 계산 (유사도 계산) 메서드 | metric_type=’COSINE’ |
| params | 각 인덱스별 별도 필요 파라미터 | params={‘nlist’:64} |
FLAT 인덱스 타입
FLAT 인덱스 타입 설명
- 고급 전처리나 데이터 구조화 없이
- <쿼리> - <데이터셋의 모든="" 벡터=""> 간 직접 비교
무차별 대입 방식에 해당- 장점 : 단순(전처리가 없음), 정확도 높음(모든 데이터셋과 비교)
- 단점 : 속도가 매우 느림 (모든 데이터와 비교하기 때문)
인덱스 생성 방법 및 파라미터
1
2
3
4
5
6
7
8
9
10
11
12
from pymilvus import MilvusClient
# Prepare index building params
index_params = MilvusClient.prepare_index_params()
index_params.add_index(
field_name="your_vector_field_name",
index_type="FLAT", # Type of the index to create
index_name="vector_index", # Name of the index to create
metric_type="L2", # Metric type used to measure similarity
params={} # 파라미터 필요 없음
)
| 파라미터 | 설명 |
|---|---|
| index_type | FLAT |
| metric_type | COSINE, L2, IP 가능 |
| params | FLAT 인덱스 타입은 별도 파라미터가 없음. |
조회(검색, 쿼리)
1
2
3
4
5
6
7
res = MilvusClient.search(
collection_name="your_collection_name", # Collection name
anns_field="vector_field", # Vector field name
data=[[0.1, 0.2, 0.3, 0.4, 0.5]], # Query vector
limit=3, # TopK results to return
search_params={"params": {}} # No additional parameters required for FLAT
)
| 파라미터 | 설명 |
|---|---|
| collection_name | 조회 대상 데이터를 보유한 컬렉션 이름 |
| anns_field | 조회 대상 인덱스 |
| data | 조회(검색)할 쿼리. 데이터셋 벡터와 동일차원의 벡터여야 함. |
| limit | 조회(검색) 결과 개수 |
| search_params | 해당 없음 |
IVF_FLAT 인덱스 타입
IVF_FLAT 인덱스 타입 설명
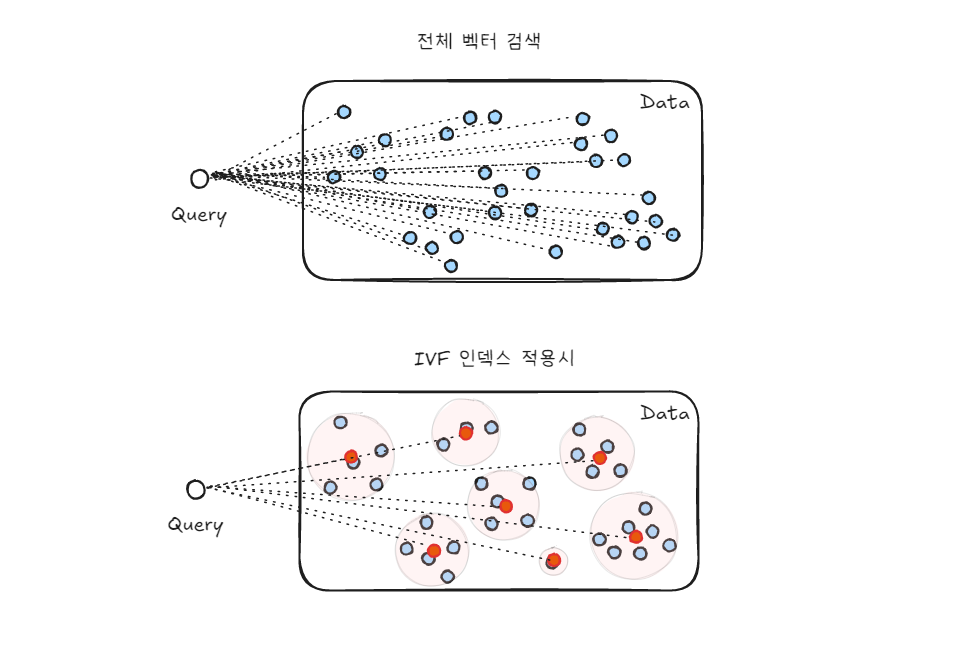
- IVF(Inverted File) : 전체 데이터를 여러 클러스터로 나누고, 쿼리와 클러스터 중심만 비교
- FLAT : 클러스터 안에서는 압축/손실 없이 원본 데이터 그대로 사용, 정확성 유지
- 대용량 데이터셋에서의 빠른 검색 + 적절한 정확도가 필요할 때 사용
인덱스 생성 방법 및 파라미터
1
2
3
4
5
6
7
8
9
10
11
12
13
14
from pymilvus import MilvusClient
# Prepare index building params
index_params = MilvusClient.prepare_index_params()
index_params.add_index(
field_name="your_vector_field_name",
index_type="IVF_FLAT", # Type of the index to create
index_name="vector_index",
metric_type="L2", # Metric type used to measure similarity
params={
"nlist": 64, # Number of clusters for the index
} # Index building params
)
| 파라미터 | 설명 |
|---|---|
| index_type | IVF_FLAT |
| metric_type | COSINE, L2, IP 가능 |
| params | nlist : 데이터셋을 몇 개의 클러스터로 분할할지 |
조회(검색, 쿼리)
1
2
3
4
5
6
7
8
9
10
11
12
13
search_params = {
"params": {
"nprobe": 10, # Number of clusters to search
}
}
res = MilvusClient.search(
collection_name="your_collection_name", # Collection name
anns_field="vector_field",
data=[[0.1, 0.2, 0.3, 0.4, 0.5]], # Query vector
limit=3, # TopK results to return
search_params=search_params
)
| 파라미터 | 설명 |
|---|---|
| collection_name | 조회 대상 데이터를 보유한 컬렉션 이름 |
| anns_field | 조회 대상 인덱스 |
| data | 조회(검색)할 쿼리. 데이터셋 벡터와 동일차원의 벡터여야 함. |
| limit | 조회(검색) 결과 개수 |
| search_params | - nprobe : 검색시 검색 대상 데이터셋을 몇 개의 클러스터로 나눌지 |
nprobe는 인덱스 생성시 지정한nlist와 동일할 필요는 없음.- 단,
nprobe<=nlist여야 함. - 예를 들어 nlist=100, nprobe=10 이면 쿼리 벡터와 가까운 10개 클러스터만 탐색함.
nprobe의 값이 높으면 더 많은 클러스터를 검색하므로 리콜향상nprobe의 값이 낮으면 적은 클러스터를 검색하므로 속도가 빨라짐.
IVF_PQ 인덱스 타입
IVF_PQ 인덱스 타입 설명
- IVF 데이터 구조 + PQ 양자화
- IVF : 상단 설명 참고.
- PQ : 프로덕트 양자화. 벡터의 정밀도를 낮춤으로써 메모리 사용량을 적게 하는 방법.
- 장점 : 메모리 사용량이 적어짐.
- 단점 : 정밀도 낮아짐.
인덱스 생성 방법 및 파라미터
1
2
3
4
5
6
7
8
9
10
11
12
13
14
from pymilvus import MilvusClient
# Prepare index building params
index_params = MilvusClient.prepare_index_params()
index_params.add_index(
field_name="your_vector_field_name",
index_type="IVF_PQ", # Type of the index to create
index_name="vector_index",
metric_type="L2", # Metric type used to measure similarity
params={
"m": 4, # Number of sub-vectors to split eahc vector into
} # Index building params
)
| 파라미터 | 설명 |
|---|---|
| index_type | IVF_PQ |
| metric_type | COSINE, L2, IP 가능 |
| params | m : 원천 벡터를 몇 개의 하위(서브) 벡터로 분할할지 |
조회(검색, 쿼리)
1
2
3
4
5
6
7
8
9
10
11
12
13
search_params = {
"params": {
"nprobe": 10, # Number of clusters to search
}
}
res = MilvusClient.search(
collection_name="your_collection_name", # Collection name
anns_field="vector_field", # Vector field name
data=[[0.1, 0.2, 0.3, 0.4, 0.5]], # Query vector
limit=3, # TopK results to return
search_params=search_params
)
| 파라미터 | 설명 |
|---|---|
| collection_name | 조회 대상 데이터를 보유한 컬렉션 이름 |
| anns_field | 조회 대상 인덱스 |
| data | 조회(검색)할 쿼리. 데이터셋 벡터와 동일차원의 벡터여야 함. |
| limit | 조회(검색) 결과 개수 |
| search_params | - nprobe : 검색할 클러스터 개수 |
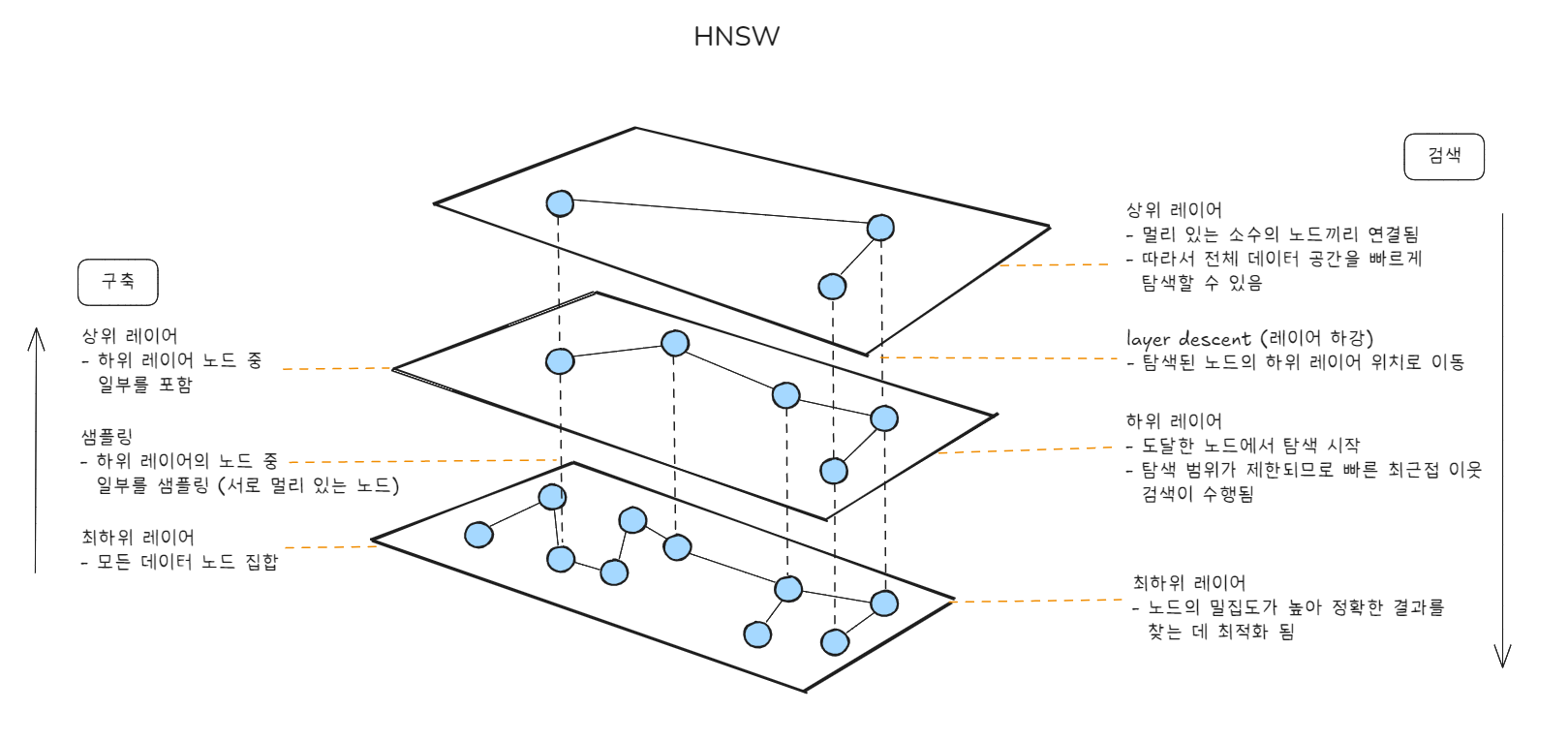
HNSW 인덱스 타입
HNSW 인덱스 설명
- 상위 레이어 - 하단 레이어(들) 구조로 구성된 계층적 데이터 구조
- 상위 레이어는 하단 레이어에서 샘플링된 데이터 포인트의 하위 집합
- 장점 : 뛰어난 검색 정확도, 빠른 속도
- 단점 : 높은 메모리 오버헤드 (계층적 그래프 구조 유지 목적)
인덱스 생성 방법 및 파라미터
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from pymilvus import MilvusClient
# Prepare index building params
index_params = MilvusClient.prepare_index_params()
index_params.add_index(
field_name="your_vector_field_name",
index_type="HNSW", # Type of the index to create
index_name="vector_index", # Name of the index to create
metric_type="L2", # Metric type used to measure similarity
params={
"M": 64, # 각 노드가 가질 수 있는 최대 연결 수(edge)
"efConstruction": 100 # HNSW 구축시 edge를 연결할 이웃 노드를 몇 개 탐색해볼지
} # Index building params
)
| 파라미터 | 설명 |
|---|---|
| index_type | IVF_PQ |
| metric_type | COSINE, L2, IP |
| params | M : 각 노드(벡터)가 연결할 최대 이웃 수- 값이 클수록 탐색 정확도 높아지는 장점 - 인덱스 구축시 메모리를 많이 사용, 연산 시간 늘어나는 단점 efConstruction : 이웃 후보 탐색 개수 (인덱스 품질)- 인덱스 구축 시 이웃 후보를 얼마나 넓게 탐색할지 - 값이 클수록 여러 이웃을 탐색하므로 인덱스 품질이 늘어나는 장점 - 인덱스 구축 속도는 느려지는 단점 하므로 |
조회(검색, 쿼리)
1
2
3
4
5
6
7
8
9
10
11
12
13
search_params = {
"params": {
"ef": 10, # Number of neighbors to consider during the search
}
}
res = MilvusClient.search(
collection_name="your_collection_name", # Collection name
anns_field="vector_field", # Vector field name
data=[[0.1, 0.2, 0.3, 0.4, 0.5]], # Query vector
limit=10, # TopK results to return
search_params=search_params
)
| 파라미터 | 설명 |
|---|---|
| collection_name | 조회 대상 데이터를 보유한 컬렉션 이름 |
| anns_field | 조회 대상 인덱스 |
| data | 조회(검색)할 쿼리. 데이터셋 벡터와 동일차원의 벡터여야 함. |
| limit | 조회(검색) 결과 개수 |
| search_params | ef : 검색 시 고려할 이웃 개수 - 높아질수록 정확도 높은 탐색 가능한 장점 - 연산 속도가 느려지는 단점 |
Vector Index의 구조
벡터 인덱스의 구조
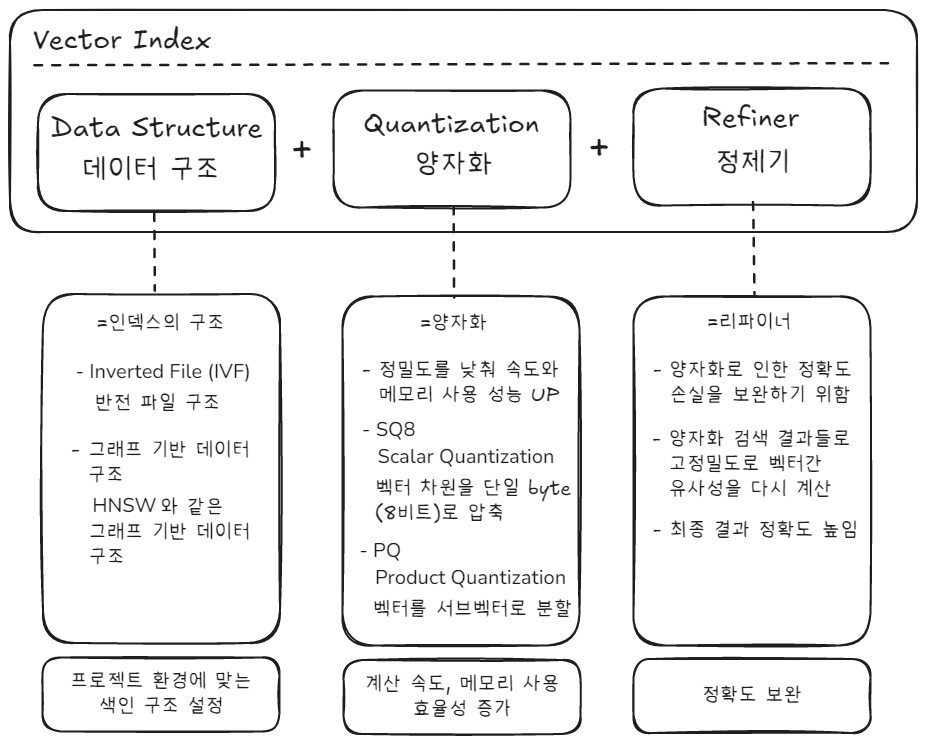
- 벡터 인덱스를 구축할 때에는 세 가지 사항을 고려해서 구축
- 데이터(인덱스) 구조, 양자화, 정제기
데이터 구조 (Data Structure)
- 인덱스의 기본적인 구조
- IVF 와 그래프 기반 구조가 있음.
| 데이터 구조 | 설명 |
|---|---|
| IVF | - Inverted File, 역파일 인덱스 - 전체 벡터를 K 개의 클러스터로 나누고 (각 클러스터는 “버킷”이라고 함) - 쿼리가 해당 버킷의 중심 벡터와 가까우면, 해당 버킷 모두와 유사하다고 판단 - 따라서, 쿼리를 모든 벡터와 비교하는 대신에 - 각 버킷의 중심 벡터들과만 비교하면 되기 때문에 계산 비용이 크게 절감 - 데이터량이 많은 대규모 데이터셋 에 적합함 |
| 데이터 구조 | 설명 |
|---|---|
| 그래프 기반 구조 | - 벡터 검색을 위한 그래프 기반 데이터 구조로 인덱스를 구축 - 가까운 이웃을 단계적으로 찾아가는 방식 - 각 벡터가 가장 가까운 이웃 벡터에 연결되는 계층형 그래프 - 고층 → 저층으로 점점 좁혀가는 계층적 탐색으로 ANN - 데이터가 고차원 이거나 빠른 검색 시간이 요구되는 경우에 적합함- 상위 레이어의 노드는 하위 레이어 노드 중 일부가 선택되어 표기됨 - |
양자화 (Quantization)
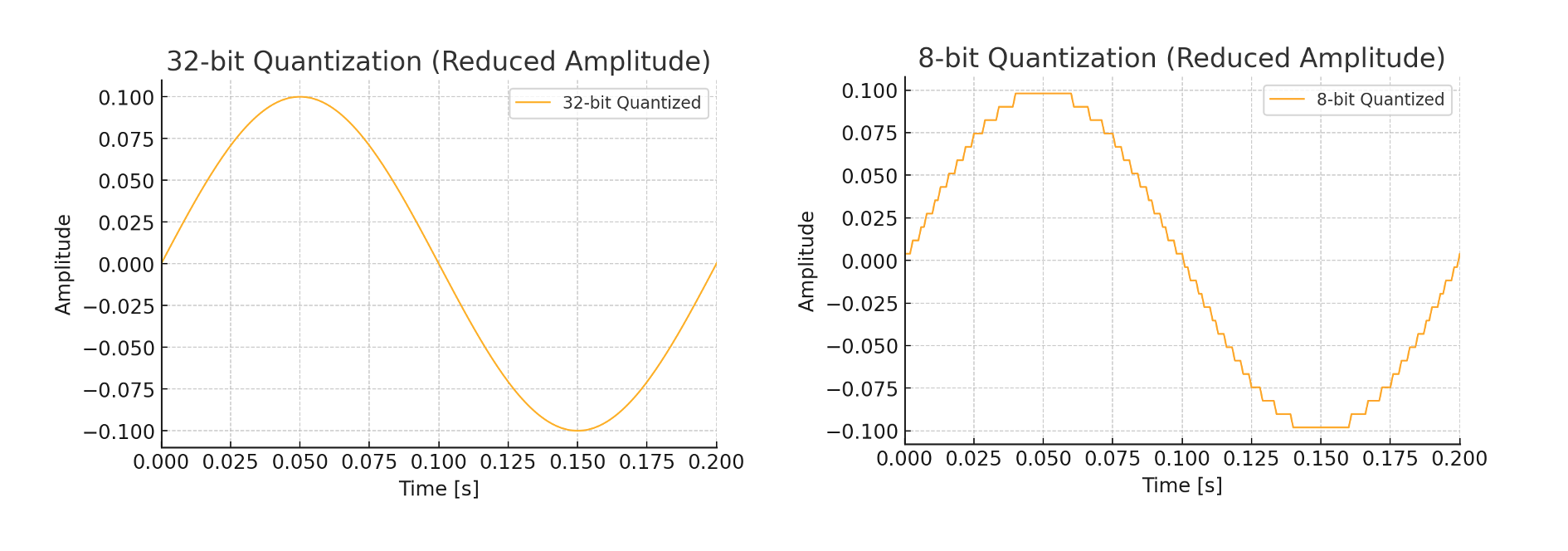
| 양자화 | 설명 |
|---|---|
| 스칼라 양자화 (SQ) | - 각 벡터 차원을 단일 바이트(8비트)로 압축 - Full Precision에 비해 메모리 사용량 75%까지 줄임 - 적절한 정확(리콜)도 유지 - 간단하고 계산 비용이 낮음 - 압축 효과는 상대적으로 낮음 - 메모리 사용량 감소는 있지만, PQ보다는 덜 효과적임 |
| 프로덕트 양자화 (PQ) | - 벡터를 서브벡터로 분할 후 각 서브벡터에 대한 별도 코드북 생성 - 코드북 : 벡터나 서브벡터들을 대표할 수 있는 작은 집합의 모음 - 각 서브벡터를 코드북의 인덱스로 표현 (대폭 압축) - 리콜을 약간 줄이면서 더 높은 압축률(예: 4~32배)을 달성 - 메모리가 제한적인 환경에 적합 - 계산은 복잡하지만, 대규모 데이터셋에서 효율적임 |
- 압축률: PQ가 SQ보다 훨씬 높은 압축률을 제공
- 성능(속도): SQ가 더 빠른 성능을 제공
- 성능(정확도): 일반적으로 SQ가 PQ보다 더 나은 리콜율을 보이나, 동일한 압축률에서는 PQ가 SQ보다 더 나은 리콜률을 제공
- 메모리 효율성: PQ는 메모리 제약 환경에서 더 효과적
리파인 (Refine)
- 양자화는 기본적으로 정밀도가 떨어져 Recall 에서 손실이 있음.
- 리파이너는 이러한 손실을 보완하기 위한 용도로 사용됨.
- 리콜 손실을 보완하기 위해서 아래와 같은 작동 방식을 가짐.
- 사소한 거리 변화가 품질에 큰 영향을 미치는 시멘틱 검색, 추천 시스템에서 중요
최종 반환할 검색 결과의 개수를 K 라고 했을 때,
(1) 양자화 단계에서 필요 이상으로 많은(K 개 이상의) 결과 후보들을 지속적으로 생성.
(2) 리파이너는 양자화보다 더 높은 정밀도를 사용해, 결과 후보들 중 상위 K 를 선택함.
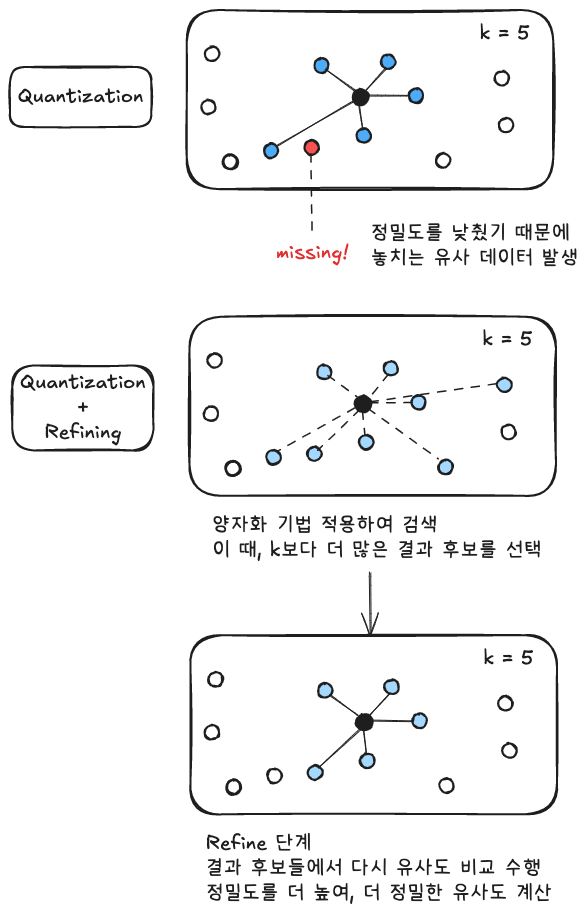
e.g.
양자화에서는 8비트 정밀도로 검색. 검색 결과 개수는 K 개보다 더 많이 반환. FP32 리파이너는 FP32 정밀도를 사용해 거리를 다시 계산해 최종 결과 K개 선택, 반환
벡터 인덱스 구조에 따른 성능 트레이드오프
인덱스 데이터 구조에 따른 초당 처리 쿼리 수
| 구분 | IVF | 그래프 기반 구조 |
|---|---|---|
| QPS (초당 쿼리 수) |
- 상위 K가 큰(2,000개 이상) 경우 그래프 기반 구조보다 우수 |
- 기본적으로 IVF보다 우수 |
인덱스 데이터 구조에 따른 검색 성능
- Top-K : 검색이 반환하는 검색 결과 레코드 개수
- Top-K 가 많다/적다의 기준 : 일반적으로 2,000개
| 구분 | IVF | 그래프 기반 구조 |
|---|---|---|
| Top-K가 작은 경우 | 리콜율에서 더 성능이 뛰어남. | |
| Top-K가 큰 경우 | 계산량에서 그래프 기반보다 효율적 | 느림 |
| 중간 크기 Top-K 높은 필터 비율 |
계산 효율이 높음 클러스터별로 걸러진 데이터만 빠르게 탐색 |
필터링 후 남은 데이터가 적어지면, 그래프 탐색 오버헤드가 커짐. |
필터 비율에 따른 Recall 향상 기법
- 필터 비율 = 스칼라 검색으로 걸러지는 데이터 비율
| 구분 | 필터링 85% 미만 | 필터링85%~95% | 필터링 98% 초과 |
|---|---|---|---|
| 인덱스 구조 | 그래프 기반 구조 권장 | IVF 구조 권장 | 무차별 대입(FLAT) 사용 |
| 이유 | 필터링 후 남은 데이터 多 -> 탐색 속도가 빠르면서 리콜율이 높은 방식 채택 |
남은 데이터 양이 적당함 이 경우 IVF 성능이 우수 |
남은 데이터 양이 적음 모두 탐색해도 무리 없음 모두 탐색하면 정확도 높음 |
양자화 방법에 따른 성능
| 구분 | SQ 스칼라 양자화 |
PQ 프로덕트 양자화 |
|---|---|---|
| 압축률 | - SQ, PQ의 압축률은 비슷 | - SQ, PQ의 압축률은 비슷 |
| Recall | - SQ보다 우수 | |
| 처리 속도 | - PQ 보다 우수 |
메모리 자원 크기와 데이터 메모리 방식
| 구분 | DiskANN | Mmap |
|---|---|---|
| 지연시간 하드웨어 자원 |
- 메모리가 원시 데이터의 1/4 미만을 감당할 수 있을 경우 사용 고려 |
- 메모리가 모든 원시데이터를 담을 수 있다면 사용 고려 |
종합적인 시나리오
| 시나리오 | 권장 인덱스 | 참고 |
|---|---|---|
| 메모리에 맞는 원시 데이터 | HNSW, IVF + 정제 | 낮은-k/높은 리콜에는 HNSW를 사용합니다. |
| 디스크, SSD의 원시 데이터 | DiskANN | 지연 시간에 민감한 쿼리에 최적입니다. |
| 디스크의 원시 데이터, 제한된 RAM | IVFPQ/SQ + mmap | 메모리와 디스크 액세스의 균형을 맞춥니다. |
| 높은 필터 비율(>95%) | 무차별 대입(FLAT) | 작은 후보 세트에 대한 인덱스 오버헤드를 방지합니다. |
대규모 k (데이터 세트의 ≥1%) |
IVF | 클러스터 가지치기로 계산을 줄입니다. |
| 매우 높은 리콜률(>99%) | 무차별 대입(FLAT) + GPU | – |

Comments