주성분분석법
주성분분석법의 개념
주성분분석법(Principal Component Analysis, PCA)은 고차원 데이터를 저차원으로 변환하는 방법 중 하나로, 데이터의 분산을 최대한 보존하면서 주요 정보를 추출하는 데 목적을 둔다.
PCA는 데이터를 구성하는 변수들 간의 상관관계를 분석하고, 데이터의 분산이 가장 큰 방향(축)을 찾아 이를 기준으로 데이터를 축소 또는 변환한다.
기본적으로 PCA는 선형 대수학적 기법을 이용하며, 데이터의 공분산 행렬을 계산한 뒤 고유치와 고유벡터를 구해 차원을 축소한다. PCA는 비지도 학습 알고리즘으로, 데이터의 레이블(클래스 정보)을 사용하지 않고 데이터 자체의 구조를 분석한다.
PCA가 활용되는 경우
(1) 차원 축소: 고차원 데이터에서 주요한 특징을 유지하면서 데이터의 복잡성을 줄이기 위해 사용된다.
(2) 노이즈 제거: 데이터를 주요 성분으로 변환하면, 잡음(Noise)을 제거하고 신호를 강화할 수 있다.
(3) 시각화: 고차원 데이터를 2차원이나 3차원으로 축소하여 데이터의 분포를 시각적으로 분석할 때 유용하다.
(4) 데이터 전처리: 다른 머신러닝 알고리즘에 적합한 입력 데이터를 생성하기 위해 데이터의 차원을 줄이고 상관관계를 제거한다.
주성분분석법의 목적
(1) 차원 축소: 입력 데이터의 차원보다 더 적은 차원의 특징을 추출하여 분석 및 계산 효율성을 높인다.
(2) 정보 유지: 변환된 데이터가 원래 데이터의 중요한 정보(분산)를 최대한 보존하도록 한다.
즉, PCA는 데이터를 단순화하면서도 중요한 정보가 유지되도록 하는 것을 목표로 한다.
변환행렬에 따른 추출 특징의 차이 (정보 손실량)
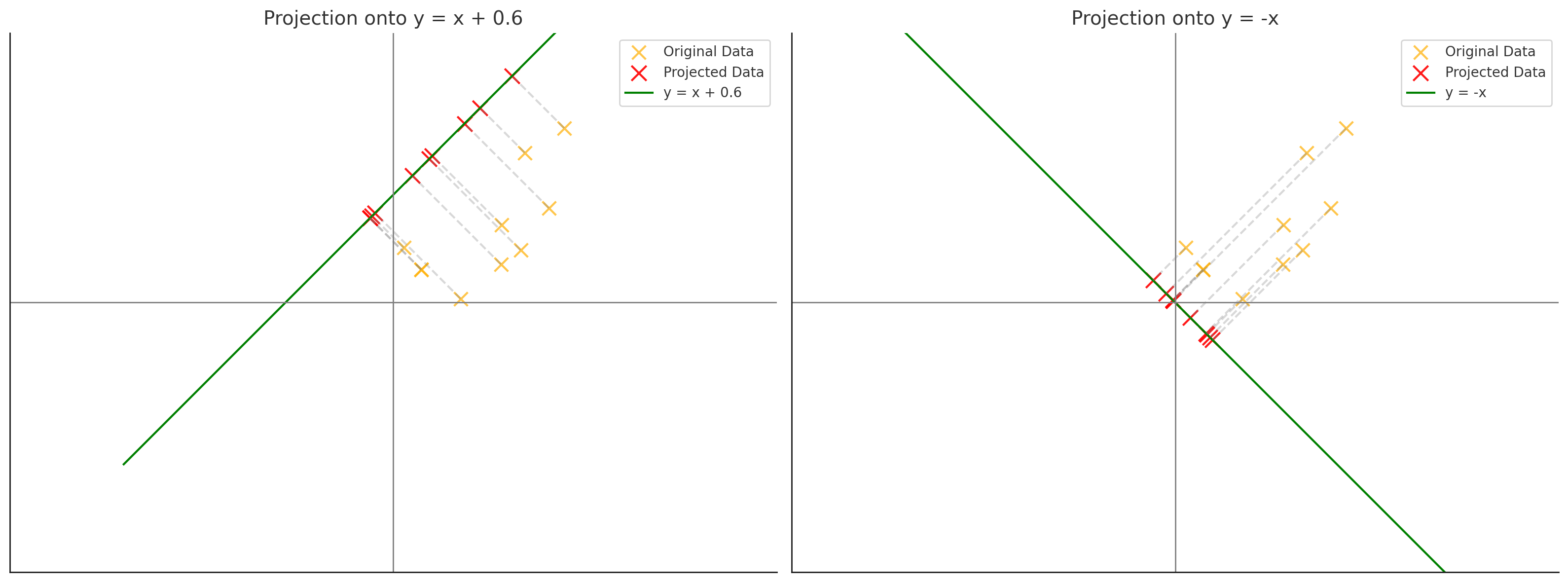
PCA에서 핵심은 데이터 집합이 가능한 한 넓게 퍼질 수 있는 방향으로 데이터를 사영(projection)하는 변환 행렬을 찾는 것이다. 이를 구체적으로 말하면, 데이터의 분산이 가장 큰 방향으로 선형 변환을 수행해야 한다는 뜻이다.
이 방향은 데이터의 공분산 행렬의 고유치와 고유벡터를 이용해 결정된다.
-고유치는 분산의 크기를 나타낸다. 즉, 가장 큰 고유치는 데이터 분산이 가장 큰 값을 나타낸다.
-그리고 이 고유치에 대응하는 고유벡터는 분산이 가장 큰 방향을 나타낸다.
수행 단계
| 순서 | 단계 | 설명 |
|---|---|---|
| 1 | 평균 및 공분산 계산 | 입력 데이터 집합 X의 평균 μₓ와 공분산 Σₓ를 계산 |
| 2 | 고유치 분석 | 고유치 분석을 통해 공분산의 고유치행렬 A와 고유벡터행렬 U를 계산 |
| 3 | 주요 고유치 선택 | 고유치가 큰 것부터 순서대로 m개의 고유치를 선택 |
| 4 | 변환행렬 생성 | 선택한 고유치에 대응되는 고유벡터를 열벡터로 가지는 변환행렬 W를 생성 |
| 5 | 선형변환 및 특징 추출 | W에 의한 선형변환으로 특징 데이터 Y를 얻음 |
차원에 따른 PCA적용의 예
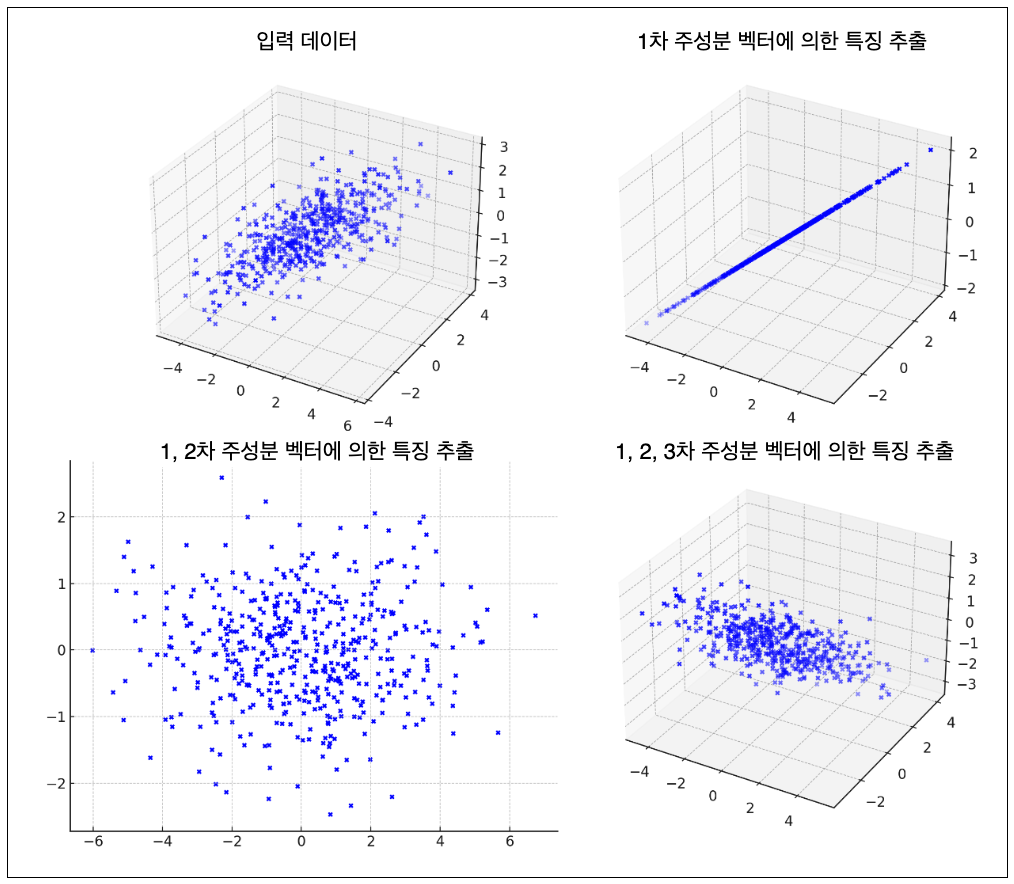
PCA의 수학적 유도
패스
주성분분석법의 특성과 문제점
(1) 입력에 대해 정보를 최대한 손실하지 않는 방향으로 차원 축소를 진행한다.
따라서, 데이터 분석에 대한 특별한 목적이 없는 경우엔 가장 합리적인 차원 축소의 기준이다.
(2) 주성분분석은 각 데이터의 클래스 레이블 정보를 활용하지 않는 비지도 학습이다.
이러한 특성 때문에 분류의 문제에서는 분류에 핵심이 되는 정보를 손실할 수 있는 결과를 초리할 수 있다. 이러한 문제를 해결하기 위해 선형판별분석법에서 클래스 정보를 활용해 분류에 핵심적인 정보를 추출하는 방향을 다음 포스팅에서 알아보도록 한다.
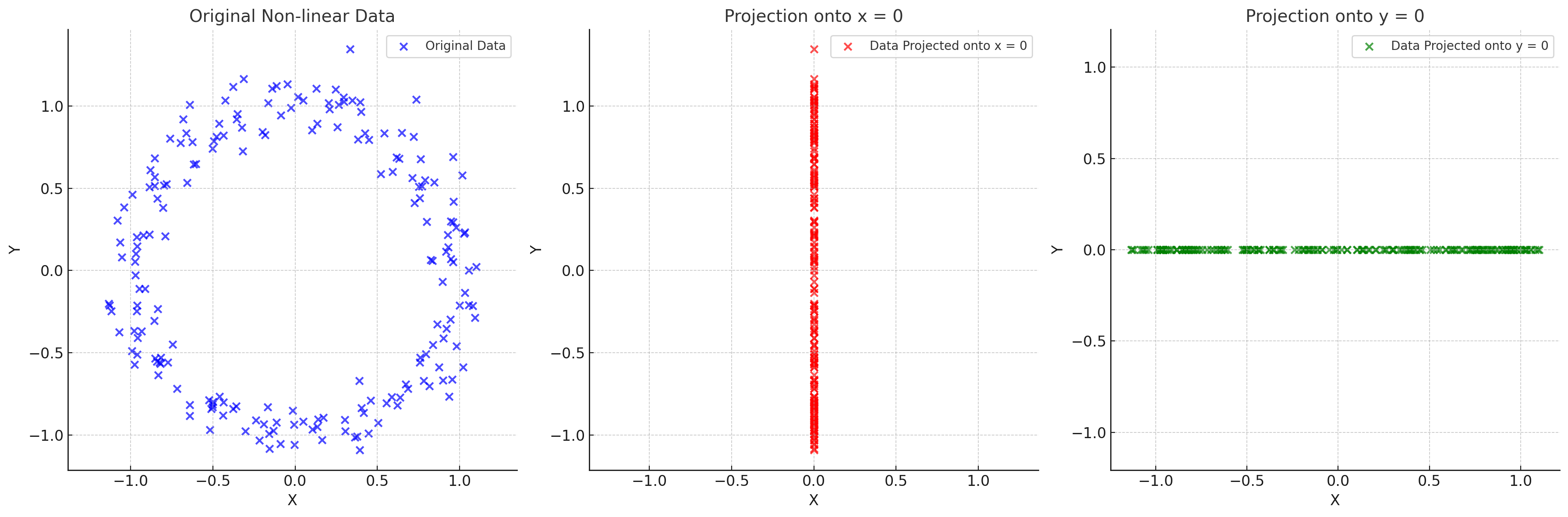
(3) 기본적으로 선형변환을 가정한다
때문에 비선형 구조를 가진 분포에 대해서는 특징을 반영하는 적절한 저차원을 찾는 게 불가능하다.


Comments