계층적 군집화
계층적 군집화의 개념
큰 군집이 작은 군집을 포함하는 형태로 계층을 이루도록 군집화를 수행하고, 그 구조를 살펴보는 방법이다. K-means 의 경우 전체 데이터를 몇 개의 배타적인 그룹으로 이루는 것과는 다른 접근 방법이다.
K-means의 경우 최적의 K 값과 적절한 초기값을 찾는 문제가 있지만, 계층적 군집화 알고리즘은 군집의 수를 미리 정해 두고 시작할 필요가 없다는 장점이 있다.
계층적 군집화 알고리즘(방법)
| 알고리즘 | 설명 |
| 병합적 방법 | - agglomerative / bottom up - 각 데이터가 하나의 군집을 이루는 최소 군집에서 시작 - 이후 가까운 군집끼리 단계적으로 병합을 진행 - 이러한 병합을 반복하면서 더 큰 군집을 만들어가는 방법 - 데이터가 n개라면 총 n-1 번의 병합 과정이 필요 |
| 분할적 방법 | - divisive / top down - 모든 데이터가 하나의 군집에 속하는 최대 군집에서 시작 - 특정 기준에 따라 군집들을 분할 - 분할 방법의 가지수가 2의 n-1제곱개 - 1개이므로 비실용적, 비현실적이다. |
이번 포스팅에서는 현실적으로 재현이 불가능한 분할적 방법 말고, 병합적 방법을 중심적으로 알아보도록 하겠다.
(1) 병합적 방법 덴드로그램
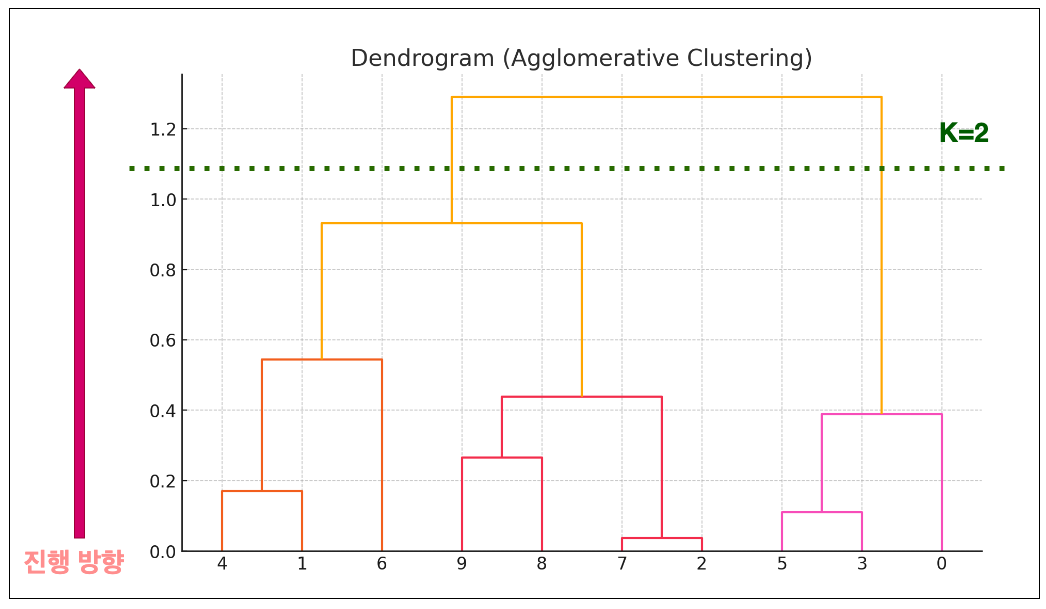
(2) 분할적 방법 예시
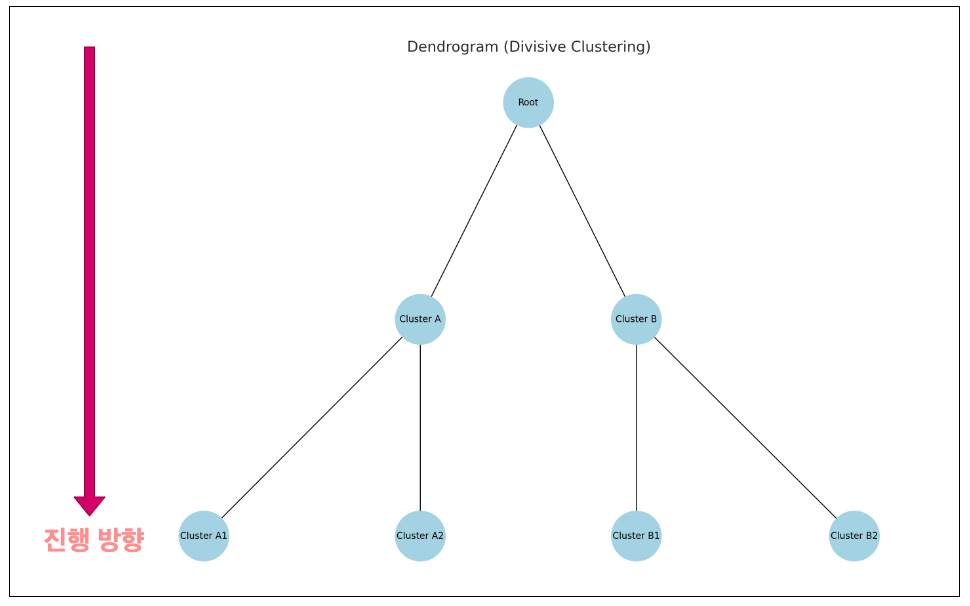
계층적 군집화의 구성 요소
| 구성 요소 | 설명 |
|---|---|
| 거리 계산 방식 (링크 결합 방식) |
데이터 혹은 군집 간의 유사성을 측정하기 위해 사용되는 방법. 종류는 아래에. |
| 적절한 군집의 수 | 덴드로그램을 통해 결정한 적절한 클러스터의 수 |
| 덴드로그램 해석 | 군집을 표현한 덴드로그램에서 수평선을 설정해 적절한 군집의 수를 결정하는 과정 |
계층적 군집화의 고려 요소
(1) 군집 간의 거리를 계산하는 방식을 어떻게 구성할 것인가
(2) 계층적 군집화를 통해 얻은 덴드로그램으로부터 어떻게 필요한 개수만큼의 군집을 찾을 것인가
알고리즘의 수행 단계(병합적 방법)
| 순서 | 단계 | 설명 |
|---|---|---|
| 1 | 초기화 | - {x1, x2 .. xn} 데이터 집합의 각 데이터가 각각의 군집이 되도록 n개의 군집{C1, C2 .. Cn}을 설정함 |
| 2 | 거리 계산 | 모든 군집들에 대해 쌍으로 군집 간의 거리를 계산한다. |
| 3 | 군집 병합 | 거리가 가장 가까운 두 군집 Ci, Cj를 선택하고 이 둘을 병합해 새로운 클러스터 Cij를 생성한다. |
| 4 | 클러스터 업데이트 | 새로운 클러스터 Cij를 클러스터 풀에 넣고, 원래 클러스터 Ci, Cj를 제거한다. |
| 5 | 반복 및 종료 | 오직 하나의 클러스터가 남을 때까지 2~5번 과정을 반복한다. |
계층적 군집화의 구성 요소
(1) 거리 계산 방식
| 거리 계산 방식 | 정의 | 특징 | 영문 |
|---|---|---|---|
| 최단 연결법 | 두 클러스터에 포함된 데이터 중 상대방의 클러스터에 가장 가까운 두 데이터 간의 거리 | 고립된 군집을 찾는 데 유용 | minimum single linkage |
| 최장 연결법 | 두 클러스터에 포함된 데이터 중 상대방의 클러스터에 가장 먼 두 데이터 간의 거리 | 응집된 군집을 찾는 데 중점을 둠 | maximum complete linkage |
| 중심 연결법 | 두 클러스터 각각의 중심(평군) 지점을 찾고, 두 클러스터의 평균 지점 간의 거리를 계산 | 특이값에 영향을 적게 받음 | centroid linkage |
| 평균 연결법 | 두 클러스터 간의 모든 데이터 포인트의 쌍(클래스1의 데이터-클래스2의 데이터)간의 거리 합의 평균 | 작은 분산을 가지는 군집을 형성함 | mean average linkage |
| Ward’s 방법 | 병합 후의 클러스터 내부의 분산값. 군집 내의 제곱합을 최소화하는 방식으로 병합한다. | 비슷한 크기의 군집을 병합함 | ward’s method |
-최단 연결법
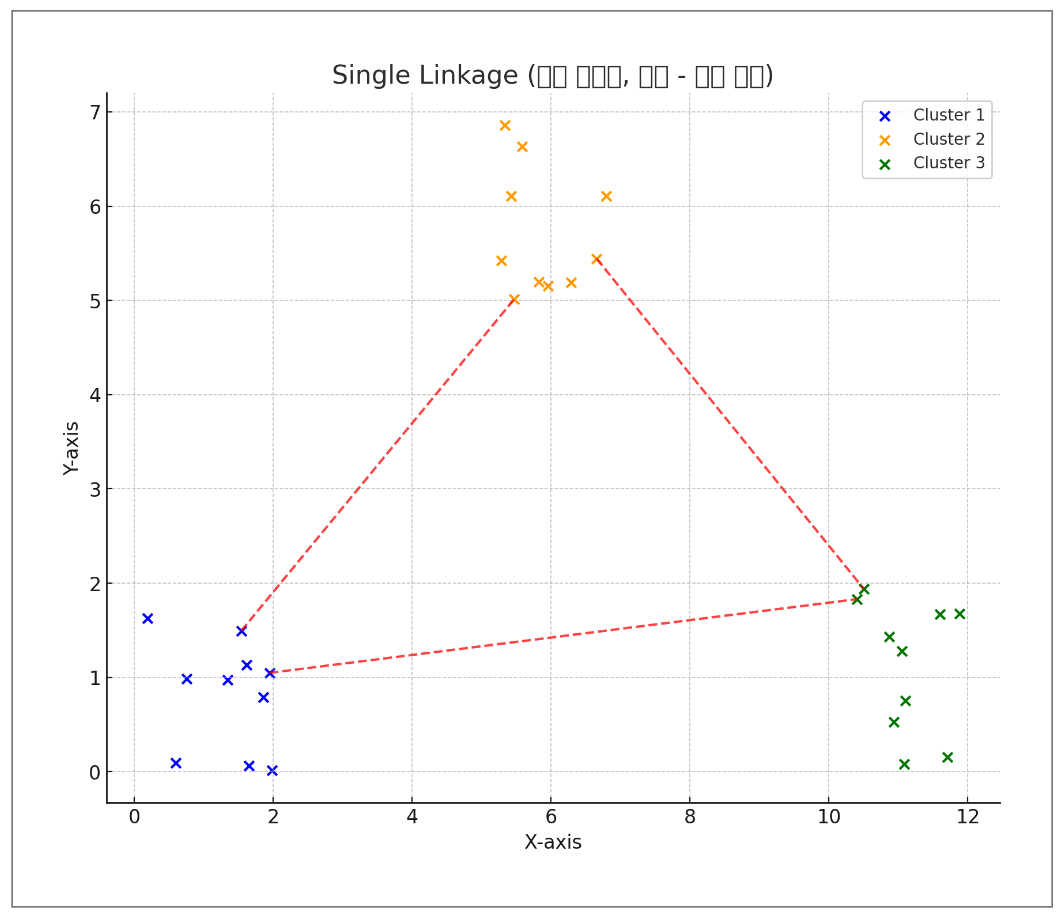
-최장 연결법
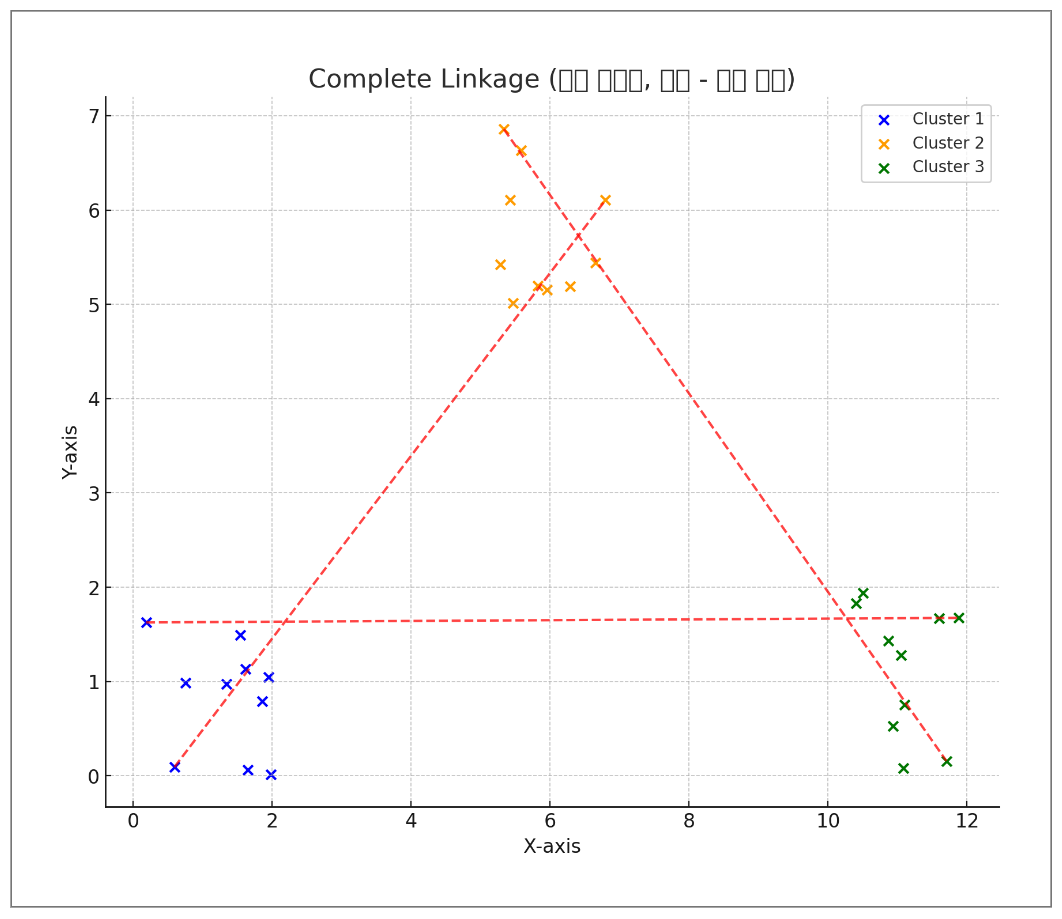
-중심 연결법
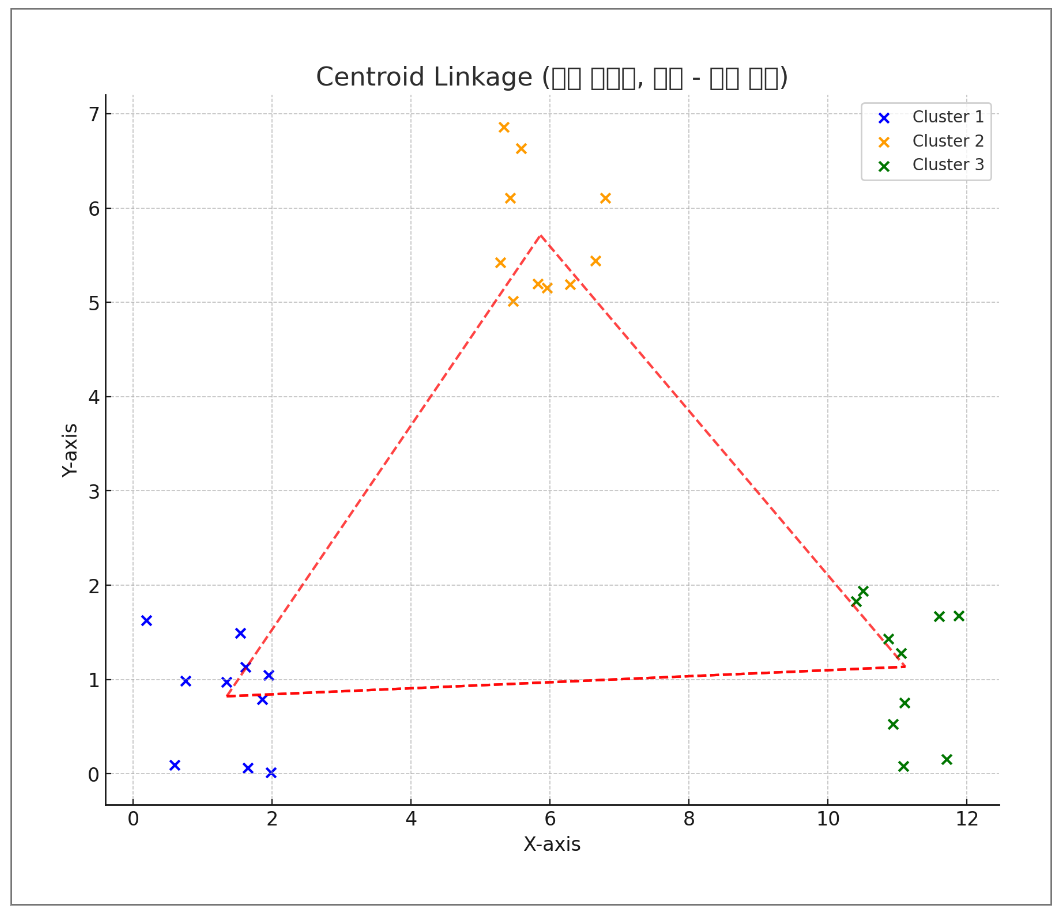
(2) 적절한 군집의 수
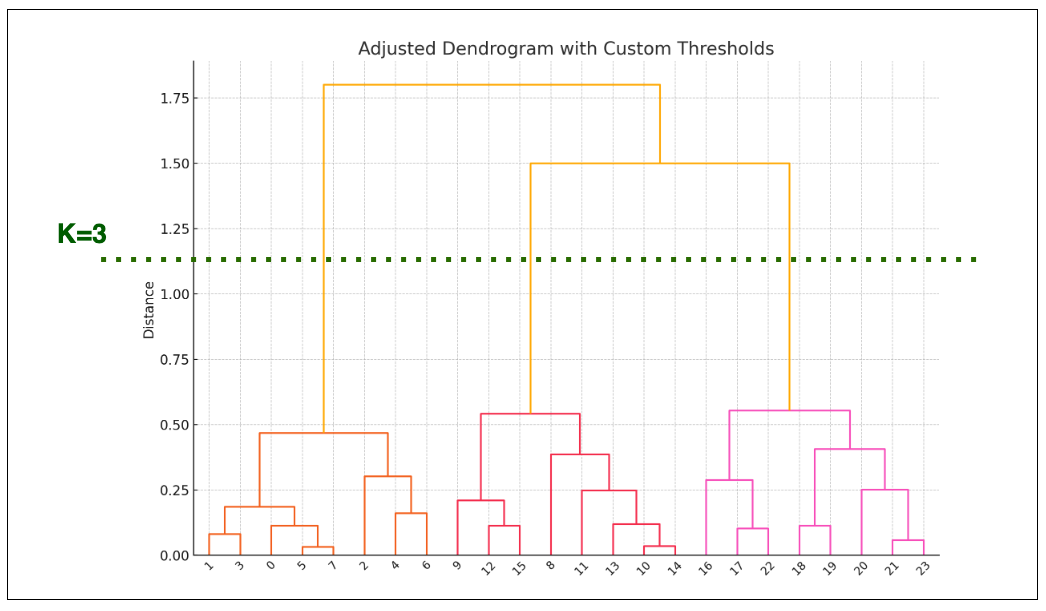
계층적 군집화에서 적절한 군집의 수를 선택하는 방법은 통합 군집에서 시작해 거리가 증가하는 동안 클러스터의 수가 늘어나지 않고 일정 기간 유지되는 지점을 찾는 것이다. 다시 말해, 계층적 군집을 통해 덴드로그램을 그리고, 1개의 군집에서부터 시작해 아래로 내려가면서 찾아지는 클러스터의 수가 일정 기간 유지되는 지점이 적절한 군집의 수 지점이라고 볼 수 있다.
위 그림에서는 데이터 군집의 수가 3개일 때가 가장 긴 기간을 유지하고 있다. 따라서 이 경우 군집의 개수를 3개로 하는 게 적절하다고 판단할 수 있다.

Comments