K-평균 군집화 알고리즘
K-means 의 개념
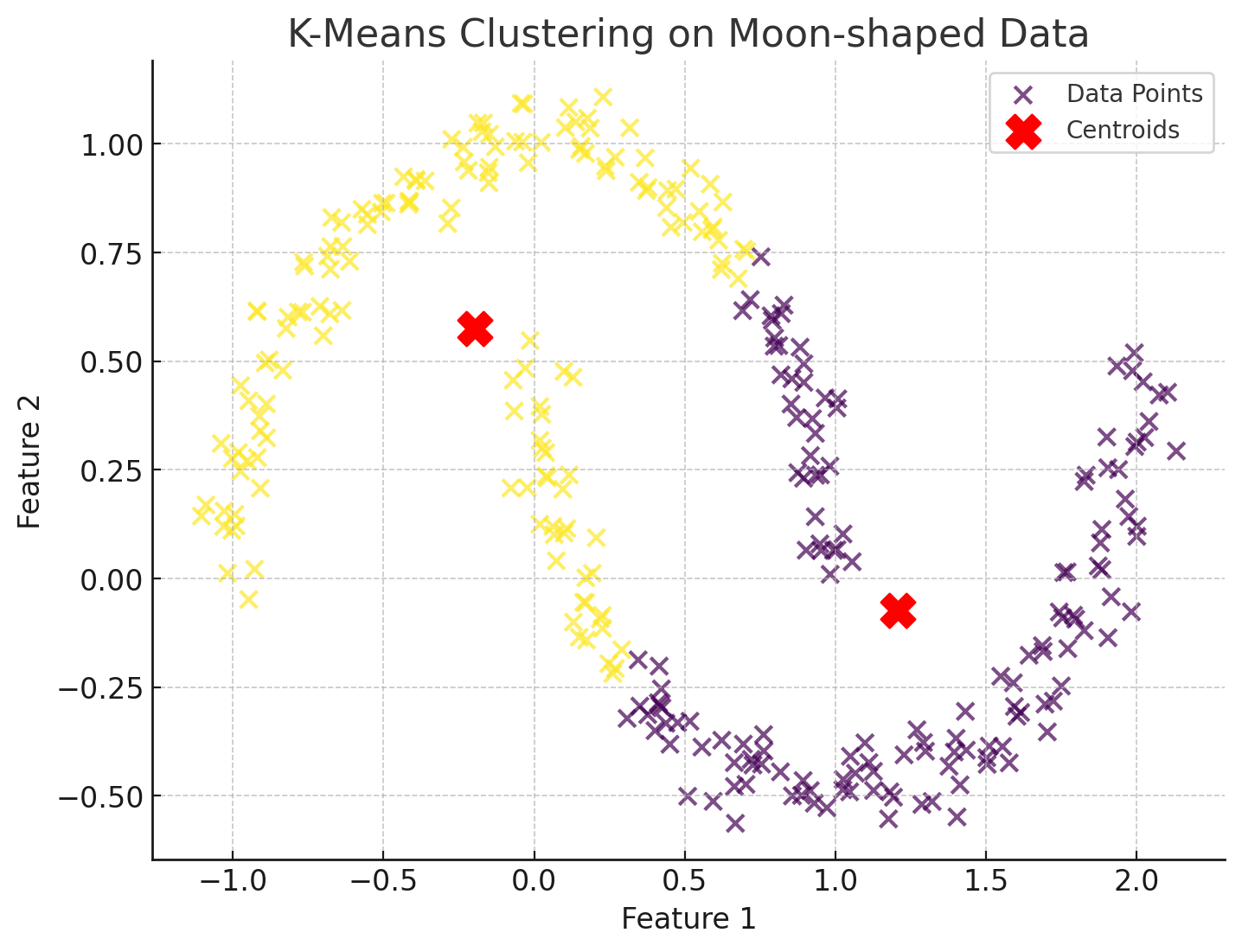
데이터 집합을 K개의 그룹으로 묶는 알고리즘이다. K개의 각 그룹은 해당 그룹 내에 속하는 데이터들의 평균을 대표 벡터로 가진다. 여기서 나오는 평균(mean) 이 바로 K-means 읙 mean을 뜻한다.
K-means 알고리즘은 구현이 간단하고, 이론적 분석도 뒷받침되어 가장 널리 사용되는 군집화 알고리즘이라고 할 수 있다. 하지만 앞으로 살펴볼 초기값의 문제, 적절한 K값의 선택 등 보장할 수 없는 한계들 또한 가지고 있다.
K-means 의 구성 요소
| 구성 요소 | 설명 |
|---|---|
| 군집 | 군집화의 결과로 나누어진 데이터 그룹. 데이터간의 유사성을 바탕으로 나뉘어진다. |
| 대표 벡터(평균, 중심) | 각 군집의 중심을 나타내는 벡터. 군집에 속한 데이터의 평균 값으로 계산된다. |
| K | 군집의 개수. 사용자가 사전에 설정한다. |
| 초기값 | 초기의 중심(대표 벡터, 평균)의 위치를 설정하는 값. 결과에 큰 영향을 미친다. |
| 반복 횟수 | 알고리즘의 종료를 결정짓는 두 가지 중 하나. 중심이 더 이상 변하지 않거나 반복횟수에 도달하면 종료된다. |
| 중심 변화 | 알고리즘의 종료를 결정짓는 두 가지 중 하나. 반복에 따라 계산된 이전 대표 벡터와 새로운 대표 벡터의 차이. 차이가 없다면 군집화는 종료된다. |
반복 횟수, 중심 변화 두 가지를 “알고리즘의 수렴 조건” 이라고 이름붙일 수 있다.
K-means 의 수행 단계
수행 단계 요약
| 순서 | 단계 | 설명 |
|---|---|---|
| 1 | 초기 중심 설정 | - 임의로 K개의 대표 벡터(중심)을 선택한다 - 이렇게 선정한 벡터들을 각 클러스터의 대표 평균값으로 설정한다. |
| 2 | 데이터 그루핑 | - 각 데이터들과 앞서 선정한 K 개의 대표 벡터들과 거리를 계산한다. - 각 데이터들에게 가장 가까운 클러스터 Ck에 속하도록 레이블링한다. - 이 과정을 통해 데이터 집합을 K개의 클러스터 C1, C2 … Ck 로 나눈다. |
| 3 | 대표 벡터 수정 | - 2번째 단계에서 나눈 각 클러스터들의 평균을 계산한다. - 계산한 평균을 새로운 대표벡터(중심)으로 삼는다. |
| 4 | 반복 여부 결정 | - 수정 전의 대표 벡터 mk와 수정 후의 대표 백터 mknew를 비교한다 - 두 벡터의 차이를 계산해, 그 값이 변화가 없거나 - 설정된 반복 횟수에 도달할 때까지 2~4번 단계를 반복한다. |
즉, K-means는 임의의 초기값으로 군집화를 진행하고, 그렇게 만들어진 군집의 평균을 구해 새로운 중심으로 삼는다. (1) 이전 군집 결과와 새로운 군집 결과의 중심 벡터의 차이가 없거나 (2) 미리 설정한 반복 횟수가 끝날 때까지 반복하여 군집화를 진행한다.
(1)
(2)
(3)
(4)
K-means 에서 고려할 문제들
고려할 사항들
| 고려 사항 | 설명 |
|---|---|
| (1) 반복 수행의 의미 | 위 단계의 반복적인 수행을 통해 좋은 군집을 찾는 것이 보장되는가? |
| (2) 초기 대표 벡터값에 대한 의존성 | 초기 대표 벡터의 설정이 군집화의 성능에 미치는 영향은? |
| (3) K값에 따른 성능 변화 | 적절한 K값을 어떻게 선택할 것인가? |
(1) 반복 수행의 의의
첫 번째 문제는 알고리즘을 반복했을 때 더 좋은 군집화(=더 잘 데이터들을 모으는지)를 보장하는가 이다. 그렇다면 “더 잘 군집화” 하는 것에 대한 정의가 되어야 한다.
“좋은 군집화”에 대한 정의는 각 클러스터 내의 데이터들이 서로 잘 뭉쳐있다. 라는 것으로 할 수 있다. 그리고 이것을 수학적으로 표현하자면 각 클러스터의 분산을 더한 값이 최소화되는 것이라고 표현할 수 있다.
여기서 군집화의 목접함수를 도출할 수 있으며 아래와 같다.
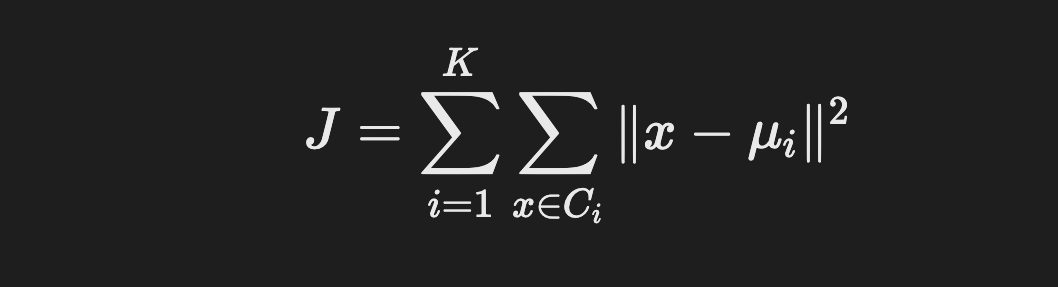
J는 각 클러스터 Ci 별로 클러스터 내의 중심과 데이터들 간의 차이를 모두 더한 값(=분산)들을 계산한 뒤, 이렇게 계산한 모든 클러스터들의 분산을 더한 값이다. 즉, K-means 는 이러한 J 값이 최소화되는 때가 데이터를 잘 군집했다고 볼 수 있다. (=데이터들이 잘 결집해있다.)
다시 말해 군집화의 목적은 이 목적함수 J 를 극소화하는 극소점을 찾는 것이 목표이다. 극소점이란, 어떠한 함수를 극소화(최소화) 하는 점을 뜻하며, 함수 전체에서의 극소점인 (1) 전역 극소점 과 지역적으로 관찰할 수 있는 (2) 지역 극소점이 있다.
K-means 알고리즘의 대표적인 벡터 수정식은 각 단계에서 최소의 파라미터를 반복적으로 찾아주는 알고리즘을 가지고 있다. 때문에 (전역 극소점을 찾는 것은 보장하지 못하지만) 알고리즘적으로 지역 극소점을 찾음을 보장한다. 그러므로 반복 수행은 군집화의 성능을 올려주는 것을 보장한다.
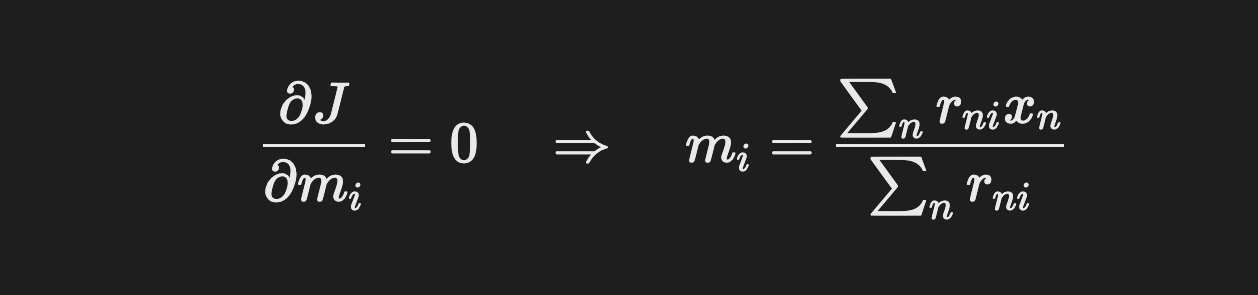
K-means의 목적함수 j 를 중심 mi에 대해 편미분한 중심 갱신식 (벡터 수정식에 해당)
(2) 초기 대표 벡터값에 대한 의존성
앞서 살펴본대로 K-means 알고리즘은 반복에 따라 극소점을 찾아감을 알 수 있었다. 하지만 전역 극소점을 찾는 것은 현실적으로 어려우므로 (목적 함수의 비볼록성, 모든 데이터에 대한 관찰이 어려움, 컴퓨팅 성능 등) 지역 극소점을 찾는 것을 보장하게 된다.
전역 극소점이 아닌 지역 극소점을 보장한다는 것은 다시 말하면 시작점에 따라 최종적으로 도출하는 해(답)이 달라질 수 있음을 의미한다. K-means 관점으로 설명하자면 초기 대표 벡터값에 따라 결과와 성능이 달라질 수 있다는 말이다.

예를 들어 초기에 선택된 데이터들이 전체 집합에서 특정 영역에 모두 몰려 있으면 최종적으로 군집화의 결과가 좋지 못할 것이고, 적절한 클러스터를 찾는 데까지 걸리는 반복 횟수가 많아지거나 심한 경우 적절한 클러스터를 찾지 못하는 경우도 발생할 수 있다.
따라서 초기값을 잘 선택해주는 것이 좋은 군집화 결과를 얻기 위해 매우 중요한 과정이며, 일반적으로 K-means에서 초기값을 찾는 방법들과 최적의 초기값을 찾는 방법으로 선택하는 방법은 아래와 같다. (정답은 없다.)
| 순서 | 방법 |
|---|---|
| 1 | 랜덤으로 초기값을 선정한다. |
| 2 | 거리가 가장 먼 데이터를 초기값으로 선정한다. |
| 3 | 여러 번 반복해서 선정해보고, 가장 좋은 초기값을 찾는다. (가장 많이 쓰이고, 현실적인 방법) |
(3) K값에 따른 성능 변화
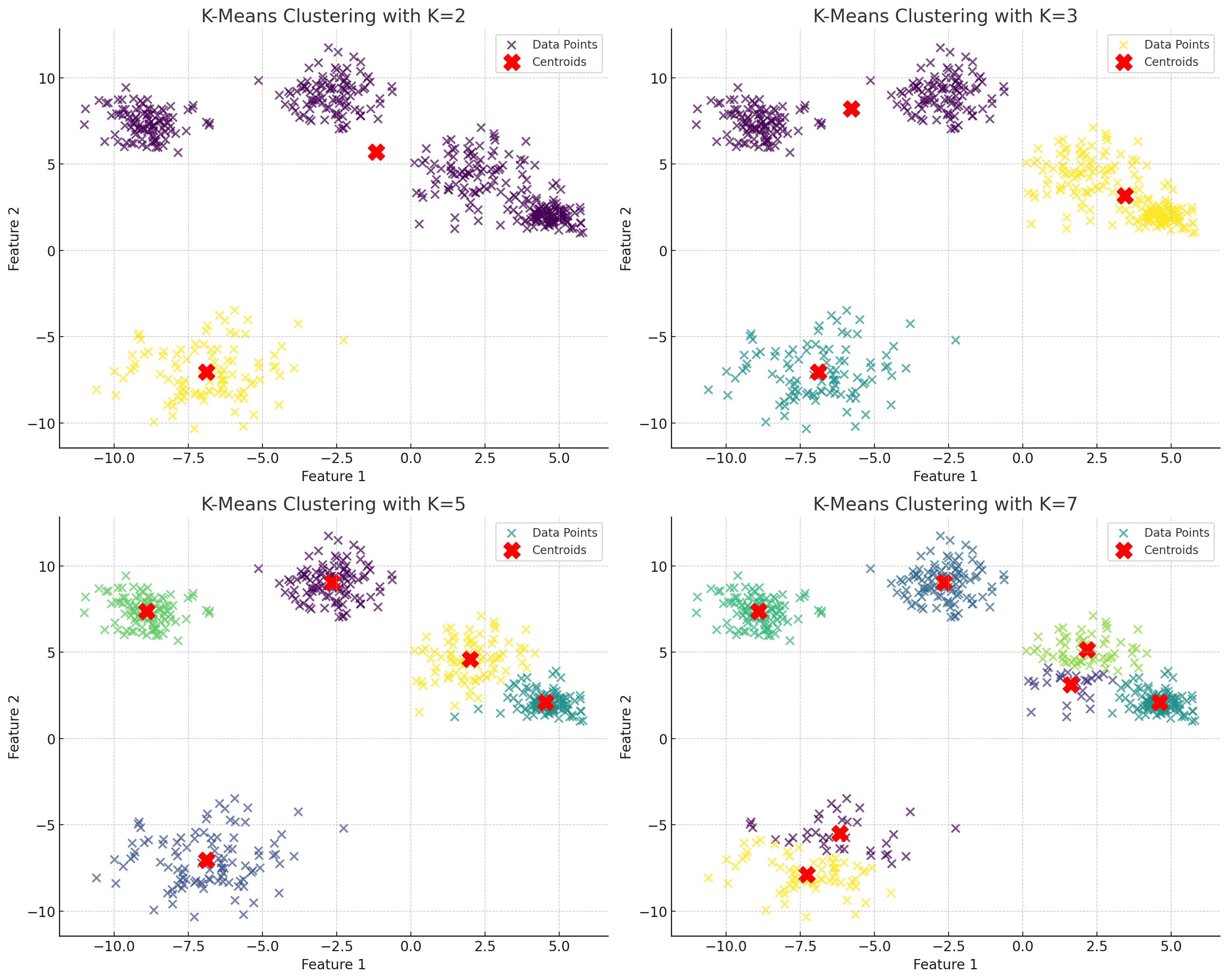
위 그림은 K 값에 따라 군집이 된 결과를 보여주고 있다. 일반적으로 군집화 문제는 정답(클래스)가 없기 때문에 잘 분류 되었는가에 대해 판단기준을 선정하는 것이 굉장히 조심스러운 문제이다. 하지만 직관적으로 평가했을 때에는 2, 7번보다는 3, 5번과 같은 군집 결과가 좋은 군집 결과로 보인다.
이처럼 군집의 성능은 K값에 따라 달라질 수 있고, 때문에 적절한 K값을 선택해주는 것은 K-means에서 굉장히 중요한 문제이다.
하지만 적절한 K 값이라는 것은 데이터(문제) 와 데이터의 분포에 지극히 의존적인 특성을 가지므로 쉽게 판단하기 어렵다. 때문에 일반적으로 적절한 K 값을 찾는 데에는 아래와 같은 방법들이 적용된다.
(1) 다양한 K값을 반복적으로 테스트해보며 적절한 K 값을 찾아감 -> 현실적이고 많이 사용됨
(2) 계층적 군집화 알고리즘으로 탐색 -> 다음 포스팅

Comments