상관관계
정의
- correlation
- 한 변수의 값의 변화에 따라 다른 변수의 분포가 달라지는 관계
- 두 변수의 값이 같이 움직이는 경향이 있는지에 대한 것
- 단, 두 변수의 값이 움직인 원인이나 순서(어떤 변수가 먼저 움직였는지)와는 무관하다.
- 상관관계가 있으면, 한 변수의 값을 이용해 다른 변수의 값을 짐작할 수 있다.
통계학에서의 상관관계
- 통계학의 많은 부분이 데이터에서 변수 간 상관관계 존재 여부를 알아내는 것이다.
- 나아가 이 상관관계의 양상이나 강도를 모델이나 수치로 표현하고, 이를 이용해 어떤 변수의 값에 대해 추론하고 예측하는 문제를 다룬다.
- 때문에 매우 중요한 개념이다.
상관관계가 있다-없다
상관관계가 있다.
- X 값의 변화에 따라 Y 값의 분포가 달라진다.
- X의 값을 알고 있다면, Y의 값이 어느 정도 값을 가질 가능성이 높은지 짐작할 수 있다.
| 구분 | 타율 | 홈런 | 타점 | 출루율 | 장타력 | 공격공헌도 |
|---|---|---|---|---|---|---|
| 연봉 | 0.255 | 0.236 | 0.162 | 0.366 | 0.231 | 0.289 |
위 상관관계 표를 기준으로, 타율이나 홈런 등 경기력 지표가 높을수록 연봉이 높을 가능성이 높다는 것을 짐작할 수 있다.
상관관계가 없다.
- X의 값이 얼마이든 간에 Y의 값의 분포는 달라지지 않는다.
- 즉, X와 Y는 서로의 값에 관계 없이 따로 움직인다.
- 즉, 변수 X와 Y는 서로 독립이다 라는 말과 같다.
- X의 값을 알더라도 Y의 값을 짐작하는 데 도움이 되지 않는다.
그래프로 보는 상관관계
상관관계가 있는 경우
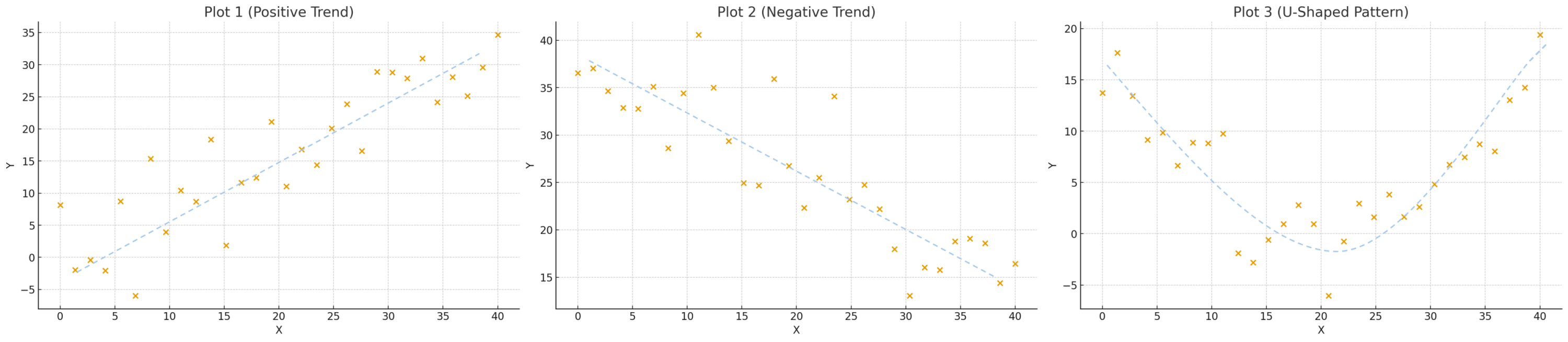
상관관계가 없는 경우
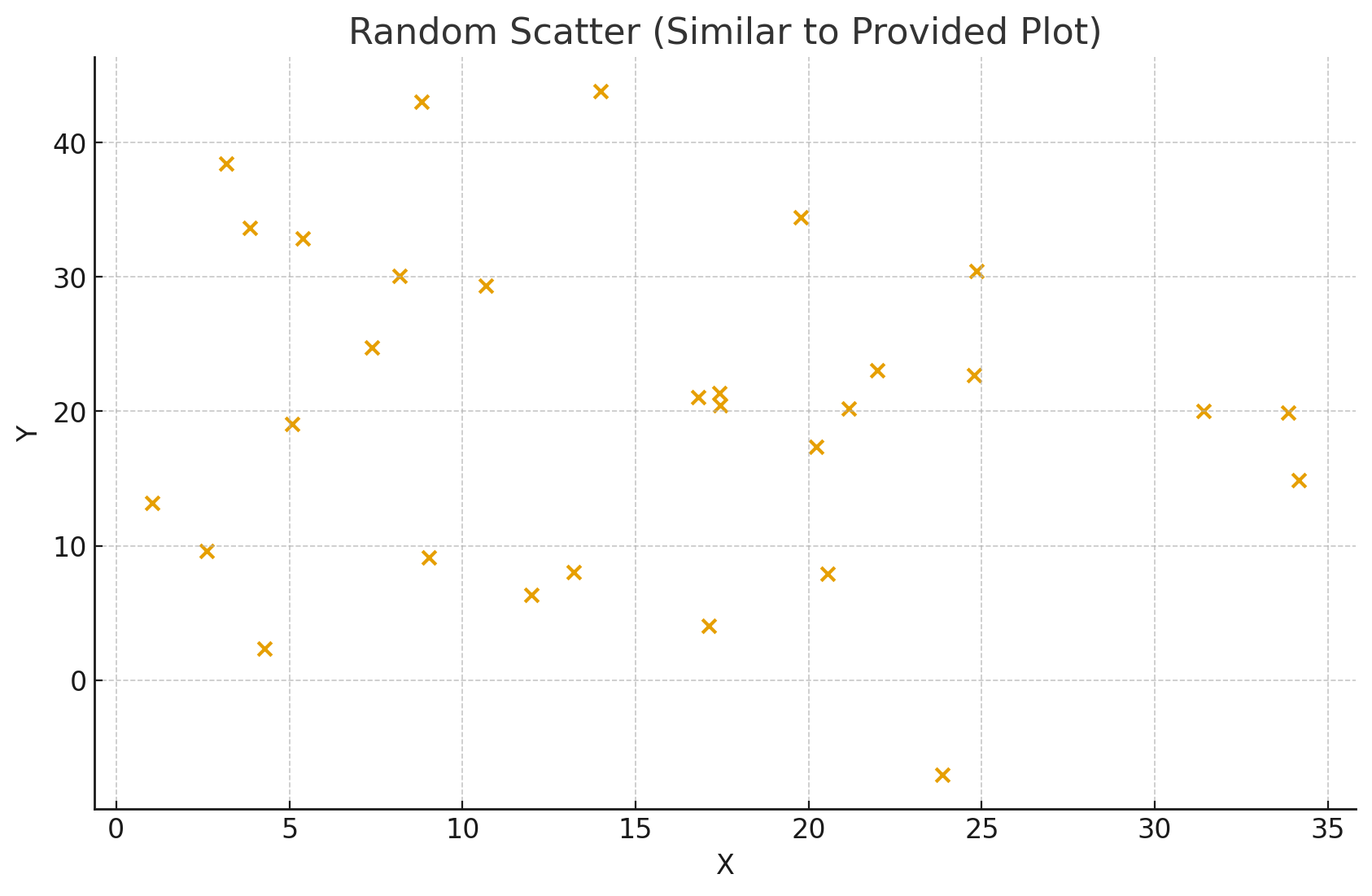
Reference
통계로 세상 읽기 - 이긍희, 이기재, 장영재, 박서영, 한종대 공저
방송통신대 - 통계로 세상 읽기 강의

Comments