통계적 추정 (statistical estimation)
정의
- 표본 데이터를 기반으로 모집단을 가장 잘 추정할 수 있는 좋은 통계량을 찾는 과정
- 모집단의 확률변수는 확률분포를 따른다고 가정한다.
- 그리고 그 분포의 모수를 가장 그럴듯하게 추측하는 추정량을 찾는 것이 목표이다.
- 즉 좋은 통계량을 찾는 것 = 좋은 추정 방법을 찾는 것 이다.
좋은 통계량의 특성
| 통계량의 특성 | 영문 | 설명 |
|---|---|---|
| 불편성 | unbiassedness | 편이(biass)가 존재하지 않는 성질 |
| 효율성 | efficiency | 밀집된 정도. 분산(흩어짐)이 적은 성질 |
| 일치성 | consistency | 표본의 크기가 커질수록 진짜 값(모수)에 가까워지는 성질 |
불편성
- 편이가 존재하지 않는 성질. 즉, 추정량의 기댓값이 모수와 정확히 같은 성질이다.
- 편이가 존재하지 않는다면, 여러 번 반복하면 평균적으로는 참값을 맞힌다는 것.
- 그리고 불편한 추정량은 불편 추정량이라고 지칭한다.
- 다만 불편하다고 항상 좋은 것은 아니다. 예를 들어, 분산의 크기가 크다면 실용성이 떨어질 수 있다.
효율성
- 밀집된 정도. 분산(흩어짐)이 적은 성질
- 흩어짐이 적다면, 결과가 흔들리지 않는 신뢰할 수 있는 추정량이 된다.
- 여러 불편 추정향 중 분산이 가장 작은 추정량을 최우수 불편 추정량이라고 한다.
일치성
- 표본의 크기가 커질수록 진짜 값(모수)에 가까워지는 성질
- 일치성이 높다는 것은 표본이 커지면 “결국에는” 정답에 가까워진다 는 의미
- 작은 표본에서는 다소 부정확할 수 있어도, $n \rightarrow \infty$ 면 정확해진다.
- 실무에서는 일치성 있는 추정량을 매우 선호한다.
예시
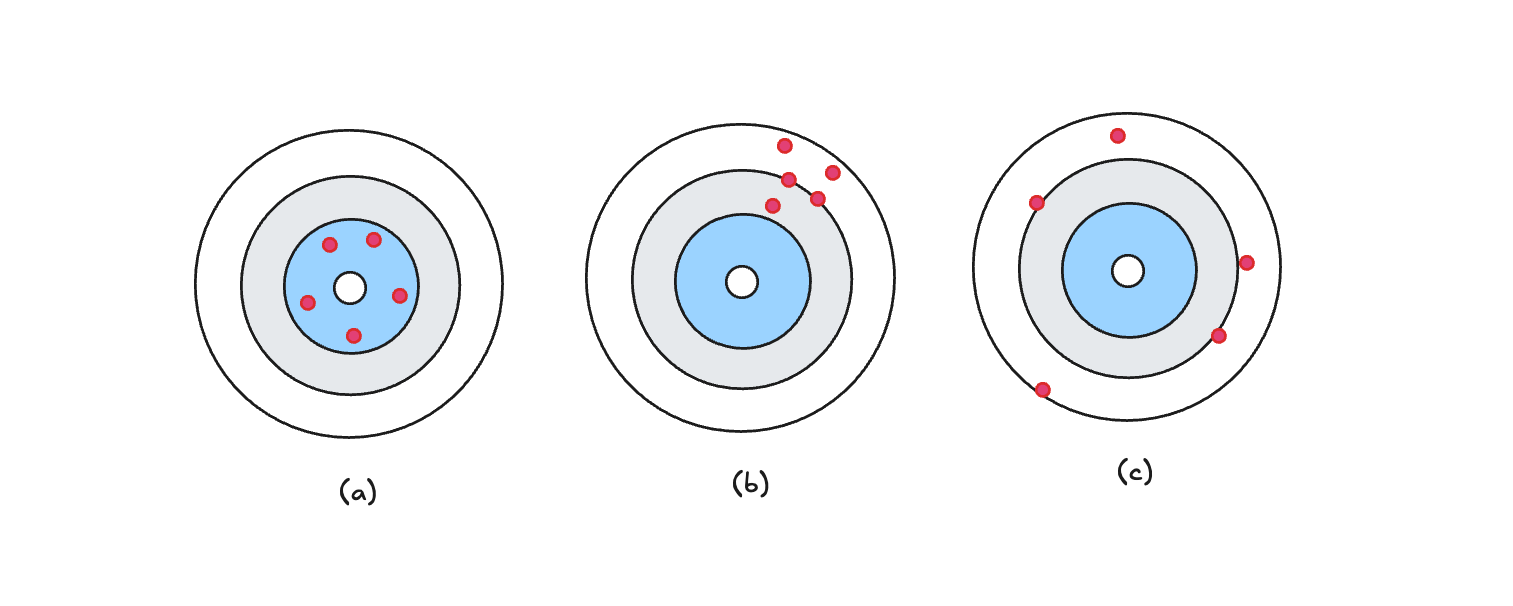
- a : 편이가 없고, 밀집도 되어있다. 불편성이 있으며, 효율성도 있다.
- b : 밀집되어있으나, 편이가 크다. 효율성은 있으나 불편성이 없다.
- c : 편이는 없으나, 밀집되어있지 않다. 불편성은 있으나, 효율성이 없다.
좋은 추정 방법
정의
- 좋은 추정이란, 모수를 최대한 정확하고 안정적으로 추정하는 가장 그럴듯한 통계량을 의미한다.
- 즉, 참값에 가깝고, 표본을 바궈도 크게 흔들리지 않으며, 편향되지 않은 추정 방법을 말한다.
- 이를 평가하는 기준은 불편성, 효율성, 일치성, 그리고 충분성이다. (충분성은 추후에 설명)
예시
- 가장 대표적인 방법이 모수에 대한 가능도 함수를 최대화하는, 가장 그럴듯한 통계량을 찾는 것이다.
- 예를 들어, 정규분포의 모평균의 경우, 가장 적합한 추정량은 표본평균이다.
추정의 결과값 유형에 따른 구분
| 구분 | 영문 | 설명 | 예시 |
|---|---|---|---|
| 점추정 | point estimation | 모집단의 모수(상수)를 하나의 값으로 추정 | 내년 성장률 3.7% |
| 구간추정 | interval estimation | 모수가 존재할 값의 범위를 추정 | 내년 성장률 3~5% |
- 점추정은 하나의 값, 구간추정은 범위.
- 구간추정에서는 신뢰구간이 동반된다.
Reference
통계로 세상 읽기 - 이긍희, 이기재, 장영재, 박서영, 한종대 공저
방송통신대 - 통계로 세상 읽기 강의
https://m.blog.naver.com/mmysmmys/222009435301

Comments