정규분포
정의
- Normal Distribution
- 데이터가 평균을 중심으로 대칭적으로 모여 있는 확률 분포
- 이를 그래프로 나타내면 그래프는 종(bell) 모양으로 나타난다.
- 평균 근처 데이터가 가장 많고, 극단값은 드물다는 특징을 가진다.
- 가우스 분포라고도 부른다. (프랑스에서는 라플라스 분포라고 부름)
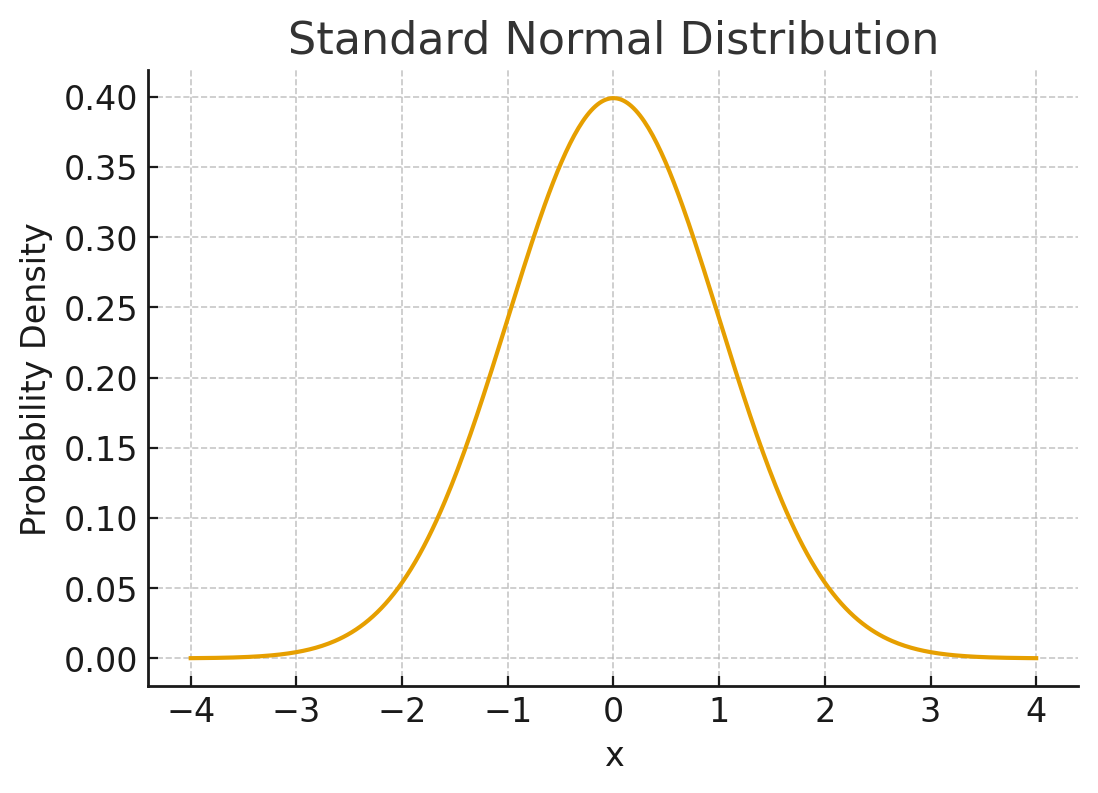
정규분포의 확률밀도함수
\[N(\mu\,, \sigma^{2}) : f(x) = \frac{1}{\sqrt{2\pi}\,\sigma} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}}\]- 평균 ($\mu$)과 분산($\sigma^{2}$)에 의해 그 모습이 정해지고, 평균을 중심으로 좌우 대칭
특징
- 정규분포에서는 평균과 중앙값, 최빈값이 같다.
역사
- 1738년 드 무아브르가 이항분포를 근사하는 정규분포의 확률밀도함수식을 발견
- 1810년 라플라스가 표본평균은 분포에 관계 없이 표본의 수가 커지면 정규분포에 근사하다라는 중심극한정리를 발견
- 1809년 가우스가 오차의 분포가 평균 중심으로 대칭적인 정규분포를 따른다고 가정하면서 본격적으로 이용했다 -> 따라서 정규분포를 가우스 분포라고 부른다.
응용
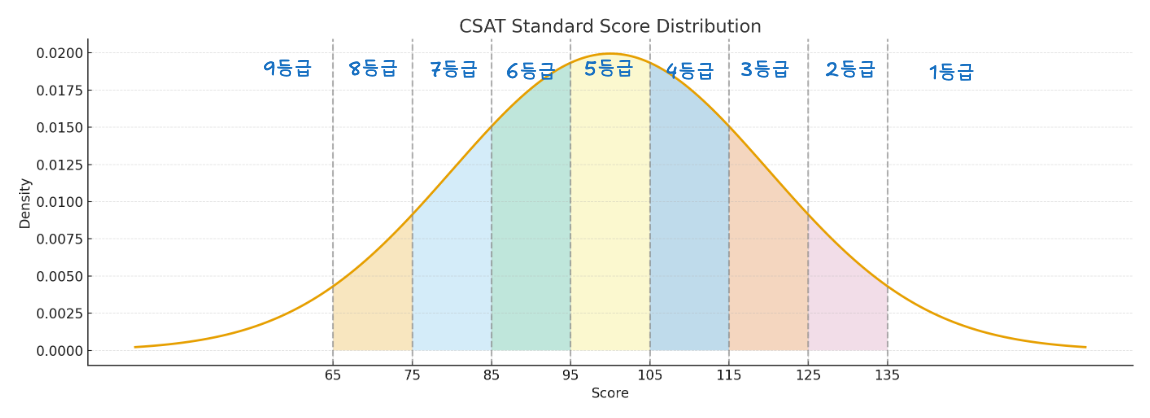
- 대학수학능력시험 등급과 해당 확률
- 사전지식 : $표준점수 = \frac{원점수 - 평규}{표준편차} * 20 + 100$
- 표준점수는 정규분포를 보인다.
| 등급 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 비율(%) | 4 | 7 | 12 | 17 | 20 | 17 | 12 | 7 | 4 |
1
2
3
P(X > 135) = P((X-100)/20 > (135-100)/20)
= P(Z > 1.75)
= 약 4%
Reference
통계로 세상 읽기 - 이긍희, 이기재, 장영재, 박서영, 한종대 공저
방송통신대 - 통계로 세상 읽기 강의
https://m.blog.naver.com/mmysmmys/222009435301

Comments