[통계] 분산

분산

정의

• 데이터가 평균에서 얼마나 벗어나는지를 제곱해 평균낸 값

계산법

표본에 대한 분산

\[s^{2} = \frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})^2\]

• (관찰값 - 평균)의 제곱합을 (데이터수 - 1)로 나눈 것

모집단에 대한 분산

\[\sigma^{2} = \frac{1}{n}\sum_{i=1}^{n}(x_i - \bar{x})^2\]

• (관찰값 - 평균)의 제곱합을 데이터수로 나눈 것

예시

데이터 : 10, 20, 30, 6, 0, -6
평균 = (10 + 20 + 30 + 6 + 0 -6)/6 = 10
분산 = ((10 - 10)^2 + (20 - 10)^2 + ... + (-6 - 10)^2)/(6 - 1)
    = ((0)^2 + (10)^2 + ... + (-16)^2)/5
    = (0 + 100 + ... + 256)/5
    = 872/5
    = 174.4

표본에 대한 분산은 왜 (데이터수 - 1)로 나누는가?

표본 평균을 사용하면 실제 모집단의 분산이 체계적으로 과소추정되기 때문이며, 이를 보정해주는 것이 (n−1)이다. 이를 자유도 보정 또는 불편 추정 이라고 부른다. 쉽게 말하면, 표본은 원래(모집단)보다 덜 퍼져(분산)보이기 때문에, 진짜 퍼짐 정도에 맞추려고 분모를 낮추는(n-1) 작업을 한다.

분산의 정의를 다시 보면, “데이터가 평균으로부터 얼마나 떨어져 있는지”를 측정하는 통계량이라는 것을 알 수 있다. 즉, 분산은 데이터가 얼마나 퍼져있는지를 뜻하는 통계량이라는 것이다.

이를 측정하기 위해, 분산 계산법에서는 각 데이터에서 평균을 뺀 값, 즉 오차 를 측정하게 된다. (오차는 계산식에서는 $x_i - \bar x$ 에 해당한다.)

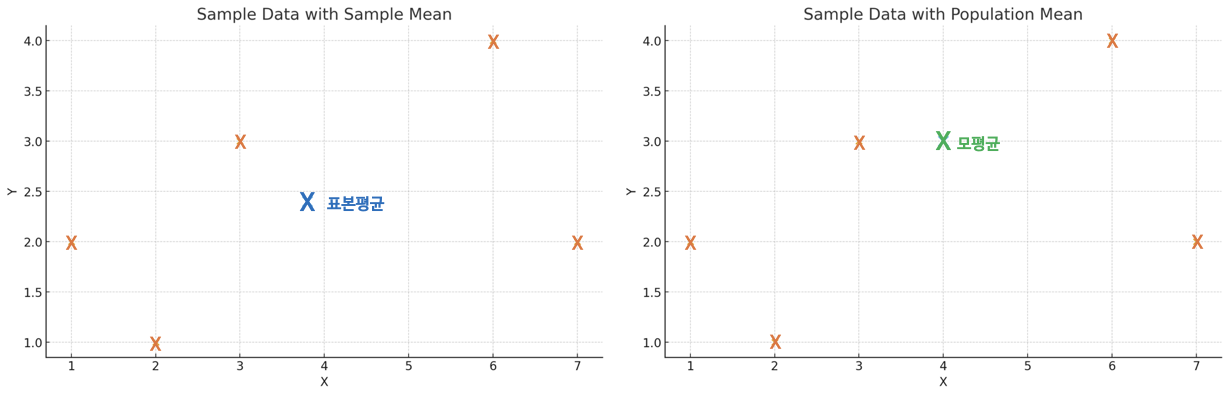
표본인 경우를 살펴보자. 표본의 평균인 표본 평균은, 해당 데이터 집합에서 가장 중심에 있는 값이다. 따라서 데이터는 표본 평균을 중심으로 오차의 제곱합이 최소가 되도록 즉, 표본 평균을 중심으로 분산이 가장 작도록 펼쳐질 수밖에 없다. 표본 데이터 집합에서 표본 평균보다 더 작은 분산값을 갖게 하는 중심위치는 없는 것이다.

반면 모집단 평균을 사용하는 경우를 살펴보자. 모집단의 평균인 모집단 평균은, 표본 평균과 같을 수도 있고, 다를 수도 있다. 불확실하다. 하지만 확실한 게 하나 있다. 모집단의 평균은 표본 평균보다 오차의 제곱합이 같거나 클 수밖에 없다. 왜그러냐면, 모집단의 평균은 표본 데이터 집단의 “가장 중심에 있는 값”이 아닐 수 있으며, 따라서 모평균을 적용한 분산은 표본평균을 적용한 분산보다 크거나 같을 수밖에 없다.

따라서 표본을 기준으로 분산을 계산할 때에는, 진짜 퍼짐 정도에 맞추기 위해 분모를 낮추어 분산을 크게 만드는 방법이 적용된다.

Reference

통계로 세상 읽기 - 이긍희, 이기재, 장영재, 박서영, 한종대 공저
방송통신대 - 통계로 세상 읽기 강의