임베딩
정의
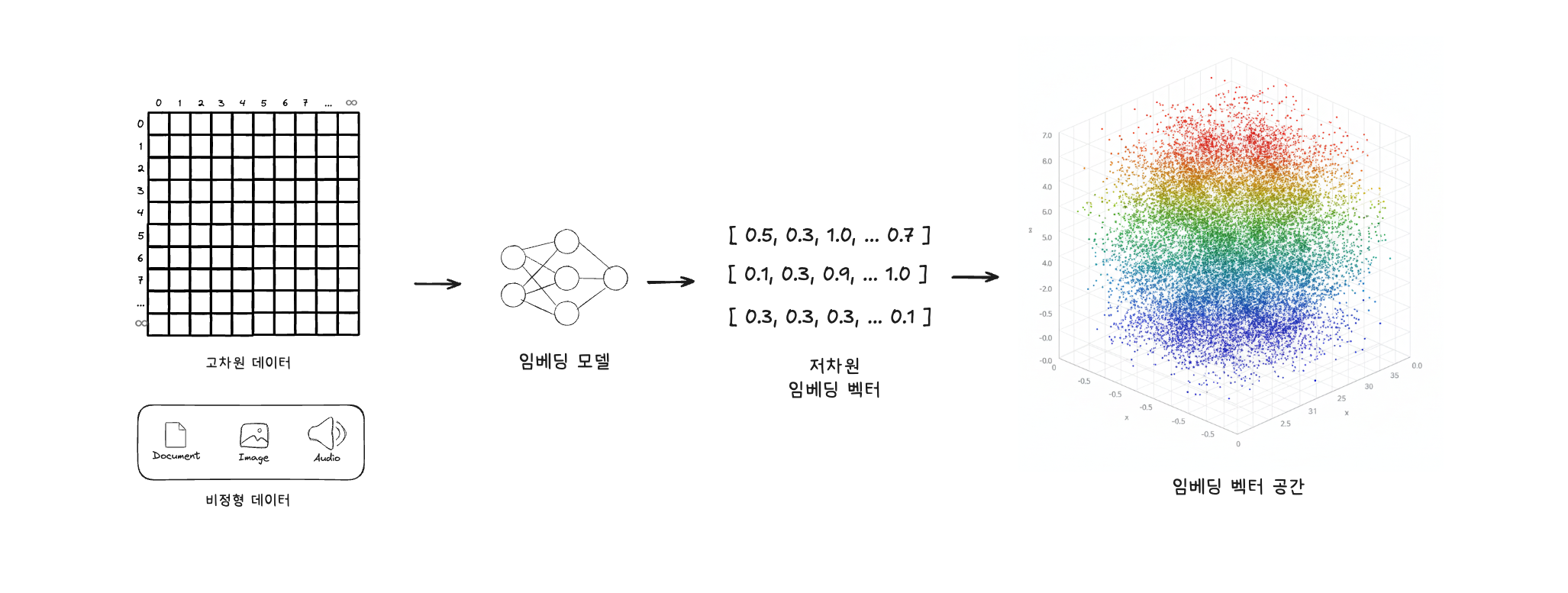
- 고차원의 데이터를, 데이터 간의 관계를 보존하면서 저차원의 연속 벡터공간으로 매핑(mapping)하는 과정
- 자연어처리 분야는 물론, 대부분의 머신러닝 분야에서 중요한 개념이다.
- 주의 : 임베딩은 변환 과정(프로세스), 결과물인 임베딩 벡터, 또는 변환을 수행하는 매핑 함수를 모두 지칭할 수 있으므로 문맥적 쓰임을 정확히 파악하는 게 중요하다.
차원 축소
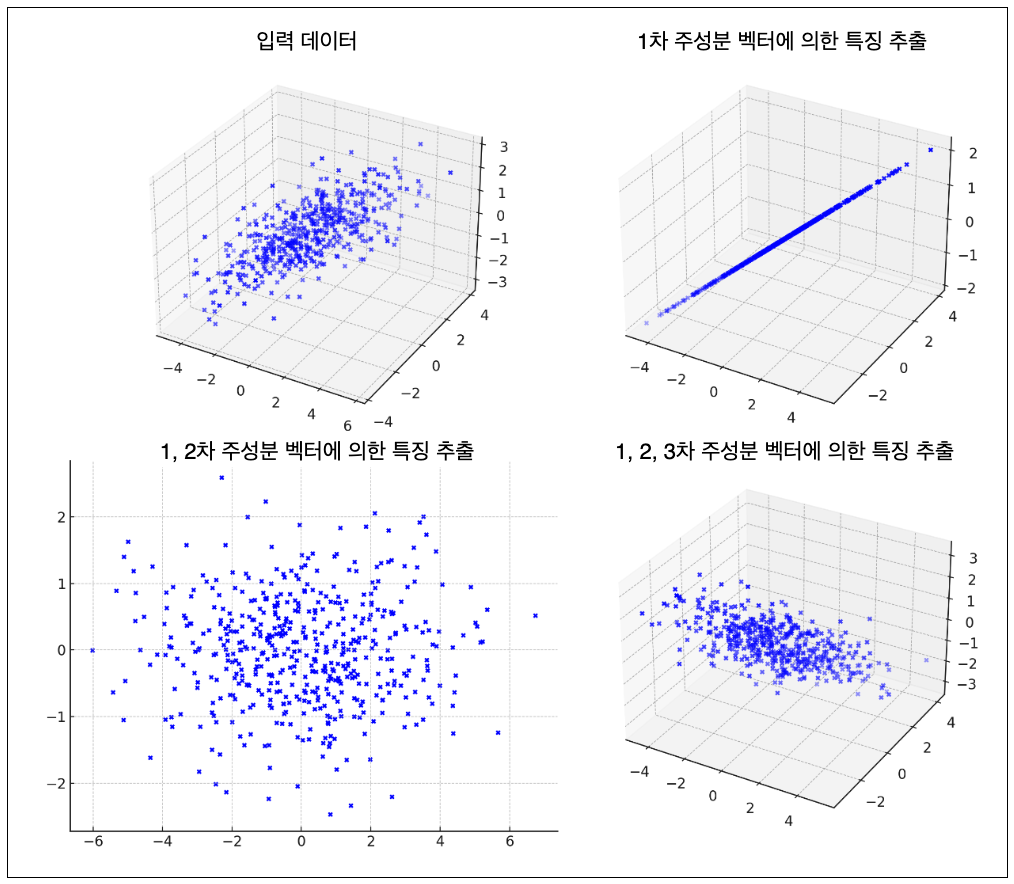
- 고차원 데이터를 저차원 데이터로 변경하는 작업을 차원 축소라고 한다.
- 차원 : 데이터를 구성하는 특성(=열)의 개수. 별도 포스팅에서 설명.
- 고차원 데이터 : 특성이 매우 많아 복잡하거나 비정형인 데이터(텍스트, 이미지, 음성 등). 현실 세계의 대부분의 데이터가 이에 해당된다.
- 저차원의 연속 벡터공간 : 실수로 구성된 숫자 벡터가 위치할 수 있는 공간으로, 이곳에 위치한 값은 컴퓨터가 효과적으로 이해하고 연산할 수 있다.
- 차원을 줄이면 계산 효율을 높이고 “차원의 저주”와 같은 문제를 방지할 수 있다.
데이터 간의 관계 보존
- 고차원 데이터를 단순한 저차원 임베딩 벡터로 변환했을 때에도, 원본 데이터가 가지고 있던 의미적 연결고리나 데이터간 유사성이 최대한 유지되어야 한다는 것이다.
- 쉽게 말해 임베딩 후에도 데이터의 의미적 특성이 잘 남아있어야 한다는 것이다.
- 임베딩에서 가장 핵심적이고 중요한 목표이다.
매핑이란
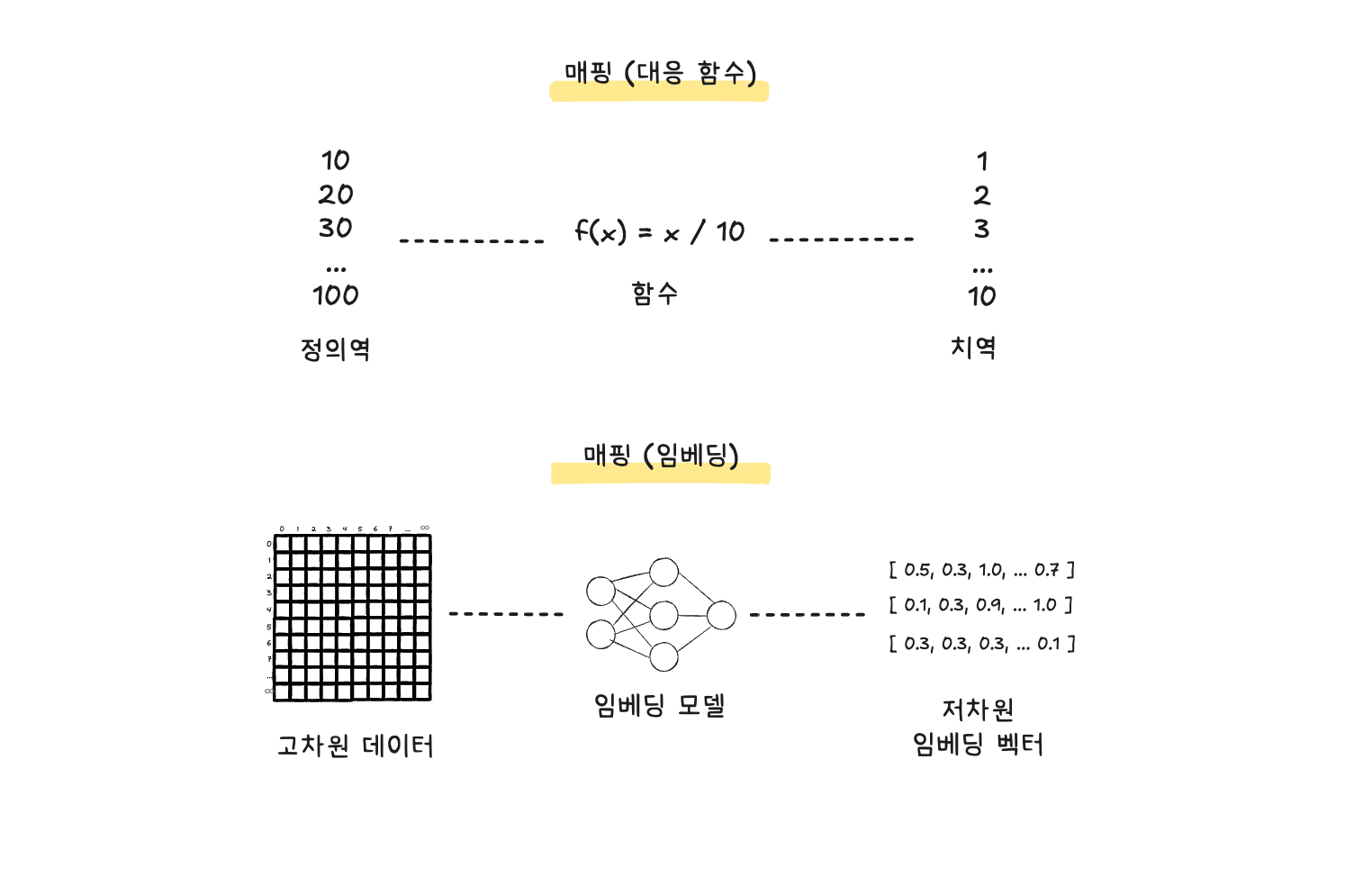
- “대응 관계” 또는 “대응 함수”라고 번역할 수 있다.
- 수학적으로, 어떤 집합의 원소를 다른 집합의 원소로 연결시키는 규칙을 가리킨다.
- 함수라고도 할 수 있는데, 함수가 미지의 값 x와 이에 대응되는 결과값을 다루는 대응 관계이기 때문이다.
- 임베딩은 고차원 데이터를 저차원 벡터로 대응시키는 매핑 과정이다.
임베딩의 필요성
- 우리가 다루는 대부분의 현실 데이터는 대부분 비정형이거나 고차원의 희소(Sparse)한 형태를 띠고 있다.
- 희소한 형태는, 데이터의 패턴을 이루는 정보가 멀리 떨어져있어 데이터의 의미를 파악하기 힘들게 한다. (=노이즈가 껴있다고도 할 수 있다.)
- 그리고 컴퓨터는 이러한 고차원, 비정형 데이터를 직접 처리하고 연산하기 힘들다.
- 임베딩은 고차원, 비정형 데이터를 컴퓨터가 효율적으로 처리할 수 있도록, 저차원의 풍부한 의미를 담고 있는 연속적인 벡터값으로 바꾸어준다.
예시 (추천 시스템): 유튜브 시청 기록 데이터가 있다고 가정해 보자. 유저가 수십억 명이고 각 유저의 시청 기록을 단순히 나열하면 매우 복잡하고 희소한 고차원 벡터가 된다. 이 데이터를 그대로 사용하면 비효율적이며 유용한 인사이트를 얻기 힘들다.
따라서 임베딩을 통해 시청 기록을 수백 차원의 임베딩 벡터로 변환하면, 시청자들의 잠재적인 패턴(예: 장르 선호도, 시청 시간대)과 같은 유용한 의미 정보가 벡터 내에 응축되어 나타난다. 이를 통해 유사한 취향의 시청자를 분류하거나 개인 맞춤형 추천을 제공하는 등 데이터를 유용하게 사용할 수 있게 된다.
임베딩이 쓰이는 곳
| 쓰임새 | 설명 |
|---|---|
| 잠재 표현 추출 latent representation |
단어, 문서, 사용자, 상품 등의 내재된 의미나 특성을 나타내는 저차원 벡터를 찾아낼 때 |
| 유사도 검색 및 추천 | 주어진 데이터(예: 문서, 상품)와 가장 의미적으로 유사한 다른 데이터(예: 유사 문서, 유사 상품)를 임베딩 벡터 간의 거리를 이용해 효율적으로 찾아낼 때 |
| 분류 모델 | 문서의 벡터를 입력받아, 해당 문서를 판단하거나 분류하는 모델을 생성할 때 |
다양체 manifold
임베딩은 언제나 가능한가?
임베딩의 개념을 접할 때 “현실 세계의 복잡한 고차원 데이터를 특성을 보존하며 저차원으로 변환하는 것이 과연 항상 가능한가?”라는 근본적인 의문이 생길 수 있다. 현재까지 딥러닝을 포함한 머신러닝의 성공 사례들은 현실의 대다수 문제에서 데이터의 상당 부분 임베딩이 가능함을 경험적으로 보여준다. 이러한 경험적 사실을 뒷받침하는 이론적 개념이 바로 다양체(Manifold)와 다양체 가설(Manifold Hypothesis)이다.
다양체의 정의
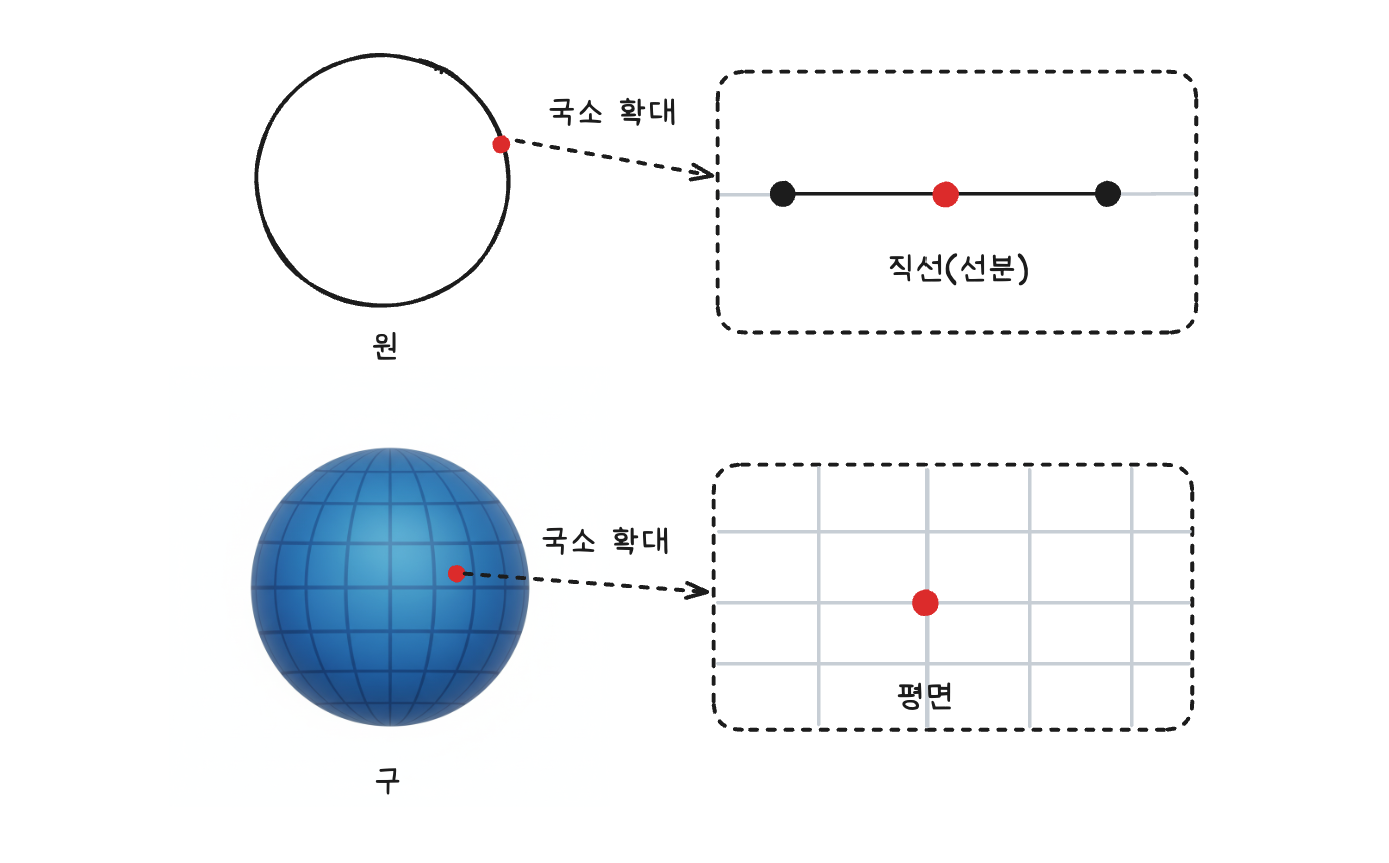
- 전체적으로는 휘어지거나 복잡한 구조를 가지지만, 국소적으로는 유클리드 공간(평평한 직선 공간)과 같은 구조를 가지는 것을 뜻한다.
- n차원 다양체 : 어떠한 공간의 임의의 한 점을 잡았을 때, 그 점 주변의 국소 영역이 n차원 유클리드 공간과 같은 위상 구조를 가지는 공간을 뜻한다.
- 1차원 다양체 : 원 -> 원의 한 점을 확대하면 인접한 점들은 직선처럼 보이는 1차원 유클리드 공간 구조를 보인다.
- 2차원 다양체 : 구, 원통 -> 곡면의 한 점을 확대하면 평평한 2차원 유클리드 공간(평면) 구조를 보인다.
다양체 가설
- 현실 세계의 데이터는 매우 높은 고차원의 공간에 존재하지만, 실제로는 그 고차원 공간 내에 놓여 있는 훨씬 더 낮은 차원의 잠재(latent) 다양체 위에 놓여 있다는 가설.
- 쉽게 말해 현실 세계 데이터의 본질적인 구조는 불필요한 노이즈 차원을 제외하면 낮은 차원으로 압축해서 표현할 수 있다라는 것이다.
- “잠재”의 의미 : 이러한 저차원 구조(다양체)가 명시적으로 보이지 않고 데이터 속에 숨어있기 때문에 잠재(latent)라는 표현이 사용되며, 머신러닝을 통해 이 잠재 구조를 찾아내야 한다.
- 성립하는가 : 사례적으로 많은 딥러닝 모델이 현실 세계에 유용하게 적용되고있다. 때문에 경험적으로 성립하며, 이는 딥러닝 모델이 고차원, 비정형 데이터를 효과적으로 학습하고 유용하게 처리할 수 있다는 이론적 근거가 된다.
- 예시 : 이미지 압축. 수만 차원의 벡터로 이루어진 이미지를 행렬분해를 통해 저차원 벡터로 표현하더라도 눈으로 보이는 품질 저하는 미미하다.
다양체 가설이 왜 성립하는가
(1) 직관적 근거
- 사람의 몸무게를 추정하기 위한 1000차원의 데이터가 있다고 가정해보자. 과연 1000가지 항목이 모두 몸무게를 결정하는 데 결정적인 역할을 할까? 반문을 해보면, 그렇지 않다는 것을 알 수 있다. 식습관, 유전 등의 특성은 강하게 작용하지만, 나머지는 중요성이 낮을 것이다.
- 일반화 하여 표현해보면, 수많은 차원으로 이루어진 데이터를 설명하기 위해 모든 데이터가 동등하게 필요할 확률보다, 일부 소수의 차원만으로 어느 정도 전체를 설명할 수 있는 확률이 더 높을 것이라는 직관적 판단을 할 수 있다. 나머지 대부분의 차원은 노이즈이거나 중복적인 정보일 가능성이 높다. 비슷한 예로 파레토 법칙(80:20 법칙)이 있다.
- 이 가설은 수학적으로 증명할 수는 없지만, 데이터 분포와 본질에 대한 우리의 일반적인 경험과 직관으로 추론할 수 있는 부분이다.
(2) 경험적 근거(딥러닝 사례)
- 딥러닝의 전제 : 딥러닝 모델은 임베딩(고차원 데이터를 관계성을 유지하며 저차원으로 변환)이 가능하다는 가설을 전제로 하고 있다.
- 딥러닝 사례들 : 자연어 처리, 컴퓨터 비전, 추천 시스템 등 현실 세계의 고차원 문제를 해결하는 딥러닝 모델들이 높은 성능을 보이며 성공적으로 작동하는 여러 사례들을 확인할 수 있다.
- 결론 : 이러한 현실적 성공 사례(딥러닝)를 통해 다양체 가설은 현실 세계 데이터에 대해 성립한다고 귀납적으로 판단할 수 있다. 따라서 충분한 데이터와 적절히 설계된 구조를 통해 임베딩 모델을 구축하고 고차원 데이터에 내재된 잠재적 저차원 구조를 추출할 수 있다라는 결론을 내릴 수 있다.
Reference
방송통신대학교 - 자연언어처리 수업 (유찬우 교수)

Comments