개념 총정리
| 개념 | 영문명 | 설명 |
|---|---|---|
| 행렬 | matrix | 수 또는 다항식 등을 직사각형 모양으로 배열한 것 |
| 행 | row | 행렬에서 가로 방향으로 나열된 집합 |
| 열 | column | 행렬에서 세로 방향으로 나열된 집합 |
| 행벡터 | row vector | 행의 수가 하나인 행렬 |
| 열벡터 | column vector | 열의 수가 하나인 행렬 |
| 정방행렬 | square matrix | 행렬의 행 수와 열 수가 같은 행렬 |
| 주대각원소 | main diagonal element | 정방행렬의 모든 (i, i) 원소들 |
| 주대각 | main diagonal | 모든 주대각 원소들을 이었을 때 만들어지는 대각선 |
| 대각행렬 | diagonal matrix | n차 정방행렬에서 i!=j인 모든 원소들이 0인 행렬 |
| 하삼각행렬 | lower triangular matrix | 주대각선 위쪽이 모두 0인 행렬 |
| 상삼각행렬 | upper triangular matrix | 주대각선 아래쪽이 모두 0인 행렬 |
| 삼각행렬 | triangular matrix | 하삼각행렬과 상삼각행렬을 묶어서 부르는 말 |
| 스칼라행렬 | scalar matrix | 정방행렬 중 주대각원소의 값이 동일한 대각행렬 |
| 단위행렬 | identity matrix | 정방행렬 중 주대각원소가 모두 1인 대각행렬 |
| 영행렬 | zero matrix | m x n 크기의 행렬 A에 대해 A + O = A 를 만족하는 행렬 O 즉, 모든 원소가 0인 행렬을 뜻한다. |
| 영행 | zero row | 모든 원소가 0인 행 |
| 음행렬 | negative matrix | 두 가지 뜻으로 해석이 가능하다. (1) 행렬에 속한 모든 원소가 음수인 행렬 (2) A + D = O 를 만족하는 행렬 D = A의 음행렬 |
| 전치행렬 | transpose of | 행열 A의 행과 열을 바꾼 행렬 AT |
| 대칭행렬 | symmetric matrix | 행렬 A와 A에 대한 전치행렬 AT 가 같은 행렬. 즉, 주대각선을 기준으로 원소가 대칭되는 행렬. |
| 반대칭행렬 (비대칭행렬) |
skew symmetric matrix | 행렬 A와 전치행렬 AT에 -1을 곱한 게 같은 행렬. AT = -A |
| 역행렬 | ||
| 정칙행렬 | ||
| 선도원소 | ||
| 행제형 행렬 | ||
| 소거 행제형 행렬 | ||
| 기본행렬 | ||
| 계수행렬 | ||
| 미지수행렬 | ||
| 상수행렬 | ||
| 확대행렬 | ||
| 닮은행렬 | 교재333 | |
| 소행렬 | 교재 109 | |
| 수반행렬 | 교재 142 | |
| 여인수 | 교재 109 | |
| 여인수전개 | 교재 109 | |
| 여인수행렬 | 교재 142 | |
| 위수 | 교재94 | |
| 유사행렬 | 교재134 | |
| 직교행렬 | 교재134 | |
| 힐버트 행렬 | 교재 72 |
행렬과 행 열
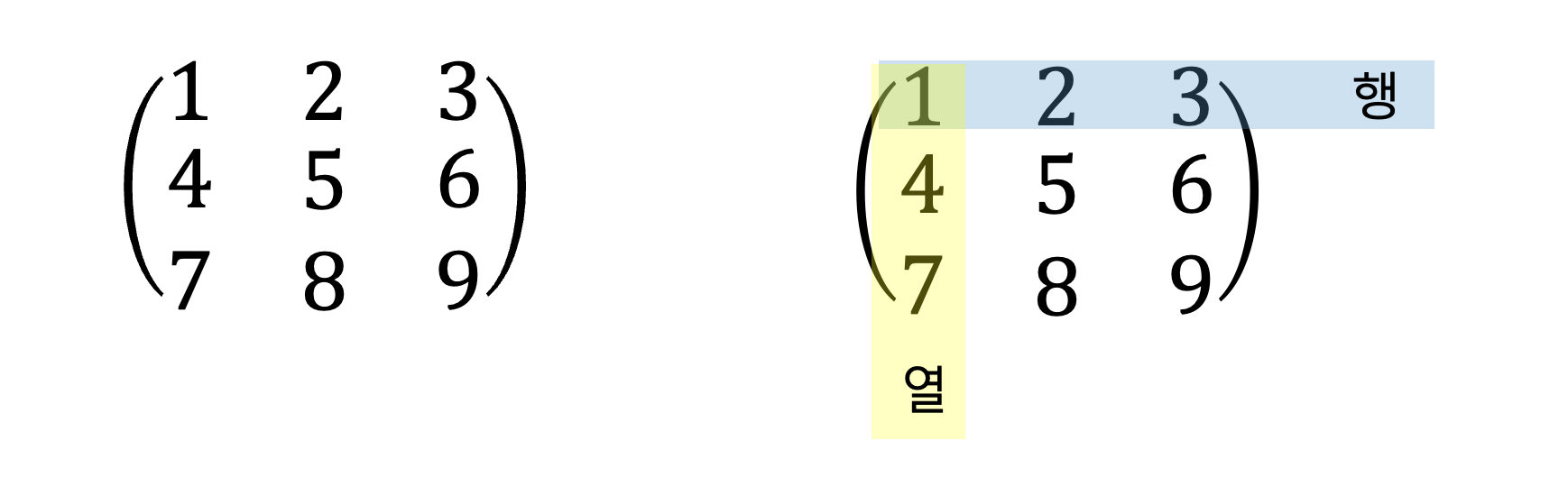
행렬은 수 또는 다항식 등을 직사각형 모양으로 배열한 것입니다. 행렬은 행과 열로 이루어져있습니다. 가로 방향으로 나열된 집합을 행, 세로 방향으로 나열된 집합을 열이라고 지칭합니다. 아래 예시와 같은 행렬에서 어떤 하나의 숫자는 각각 하나의 행과 하나의 열에 속하게 됩니다. 예를 들어 숫자 1은 1행과 1열에 속하고, 숫자 8은 3행과 2열에 속합니다.
행렬의 크기
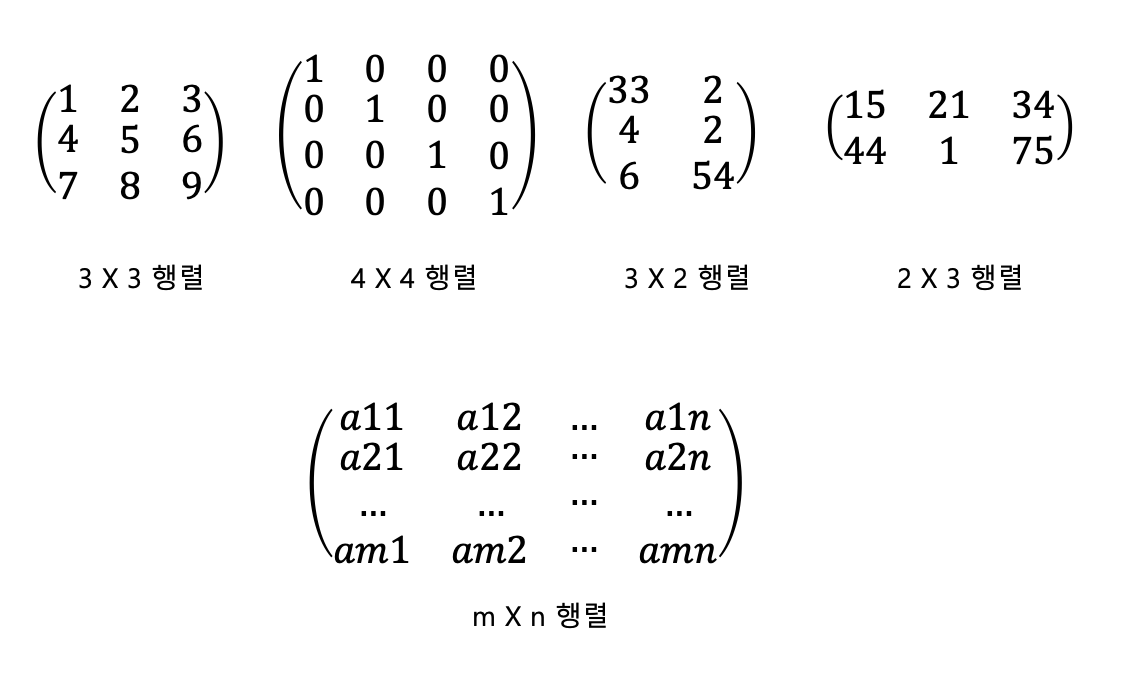
행렬의 크기는 행과 열의 개수로 표현됩니다. 3개의 행과 2개의 열을 가진 행렬은 3 X 2 행렬이라고 부르며, 이것을 일반화하면 m개의 행과 n개의 열을 가진 행렬의 크기는 m x n 이며, 이 행렬을 보통 m x n 행렬이라고 부르게 됩니다.
행렬의 원소 (성분)
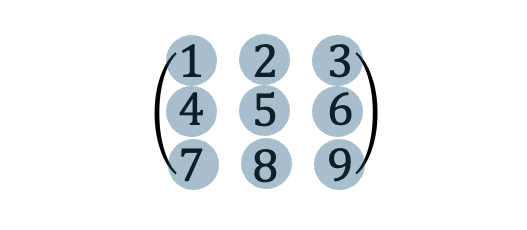
행렬에 포함되는 각 값이나 수식 등은 원소 또는 성분이라고 지칭합니다. 아래 행렬에서는 1, 2, 3, 4, 5, 6, 7, 8, 9 가는 숫자 값을 가진 원소들이 포함되어있음을 볼 수 있습니다.
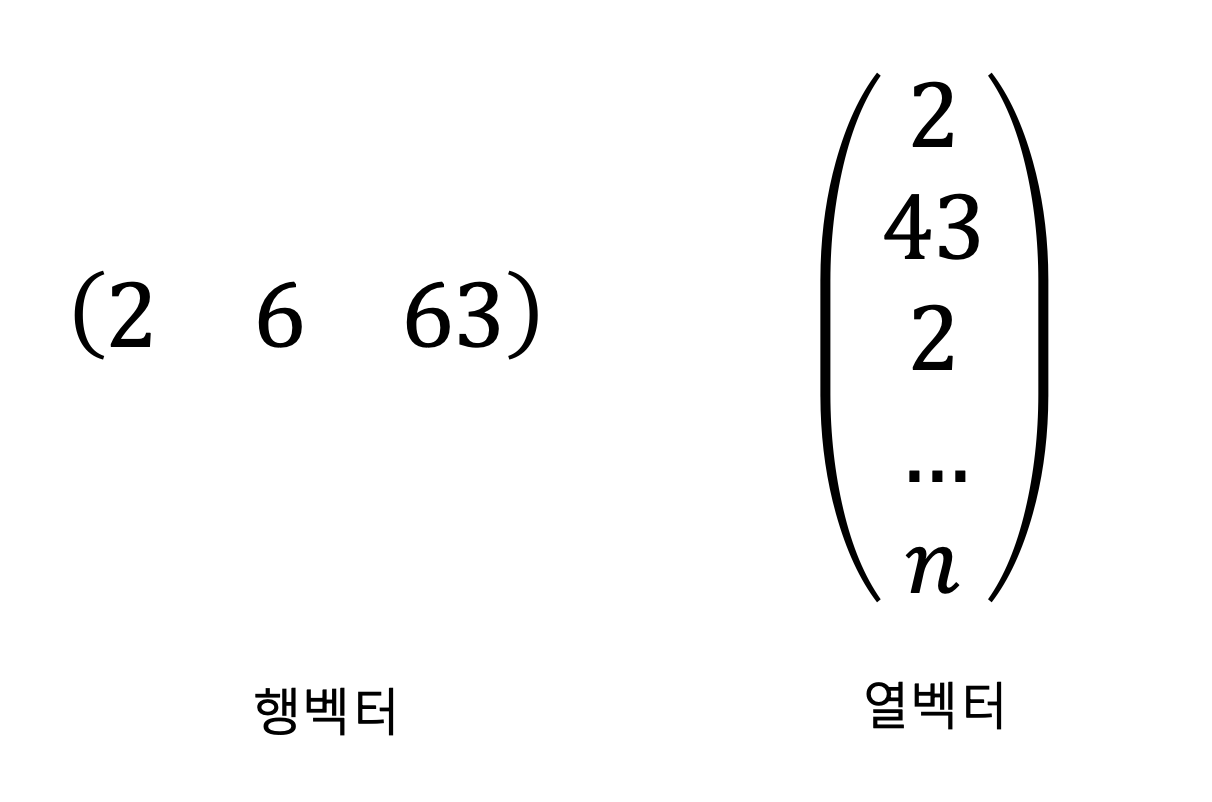
행벡터와 열벡터
| 구분 | 설명 |
|---|---|
| 행벡터 | 행의 수가 하나인 행렬 |
| 열벡터 | 열의 수가 하나인 행렬 |
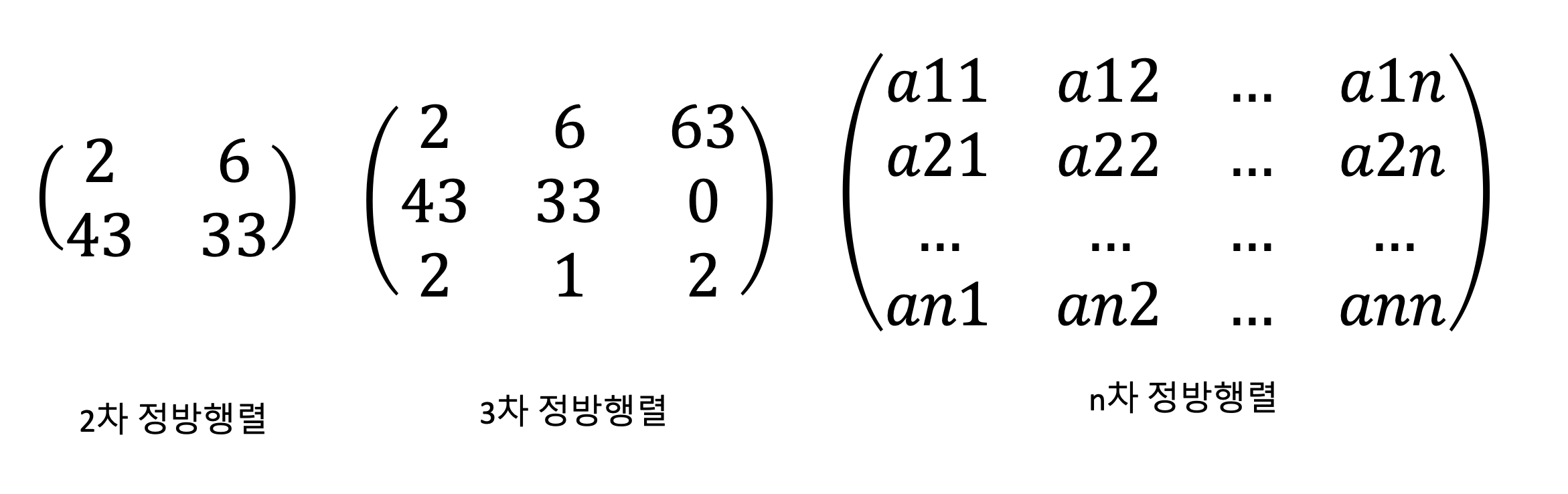
정방행렬
행렬 A를 m x n 행렬이라고 할 때 A의 i번째 행의 j번째 원소를 A의 (i, j) 원소라고 합니다. (단 1<= i <= m, 1 <= j <= n) 만일 m = n 이면 A를 차수가 n인 정방행렬 또는 n차 정방행렬(square matrix of order n)이라고 합니다.
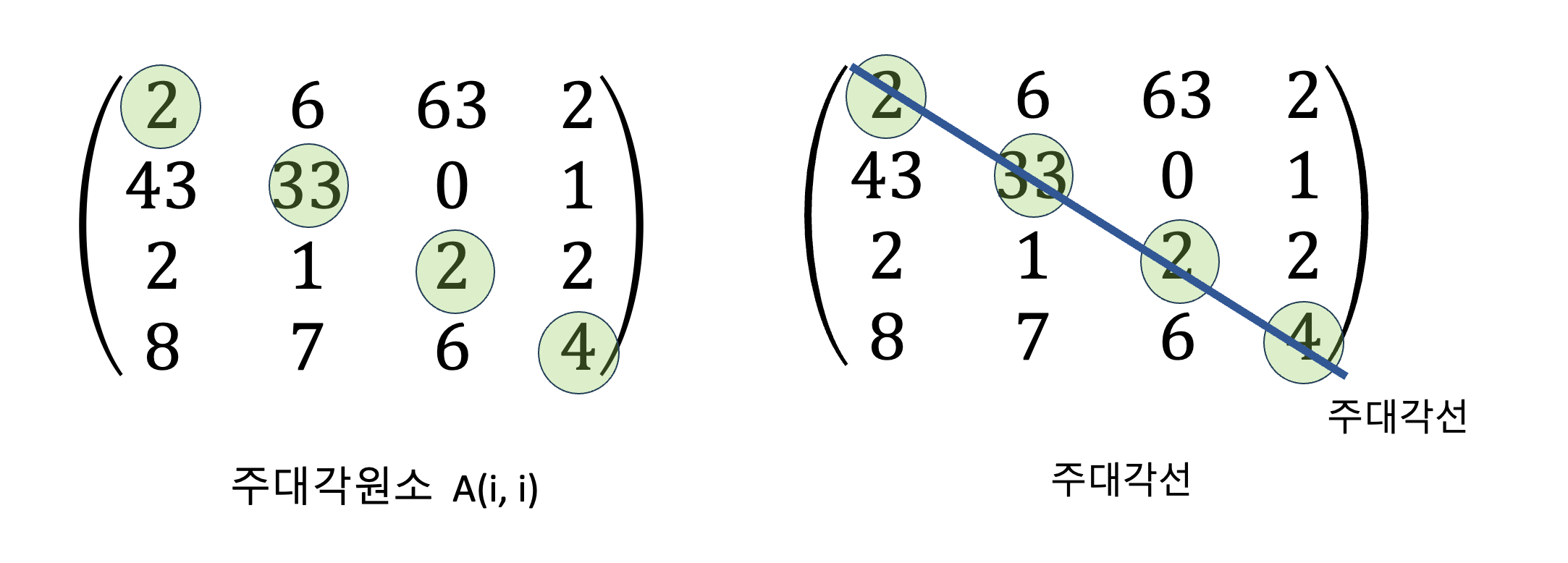
주대각 원소와 주대각선
n차 정방행렬에서 A의 모든 (i, i) 원소 (단 1<= i <= n)를 주대각 원소라고 하며, 이 원소들을 이은 대각선을 주대각선이라고 합니다.
대각행렬과 삼각행렬
대각행렬
n차 정방행렬에서 i!=j인 모든 원소들이 0인 행렬.
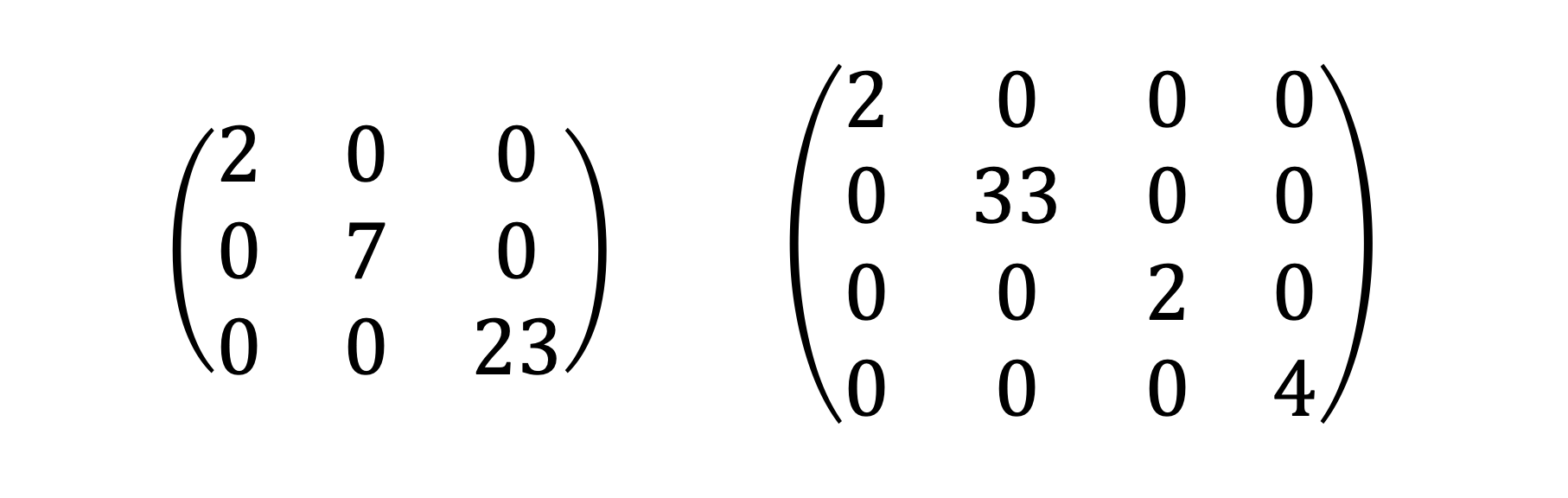
하삼각행렬
대각선 위쪽이 모두 0인 행렬. 0이 아닌 원소가 있다면 주대각선과 대각선 아래 삼각에 있기 때문에 하삼각 행렬이라고 합니다.
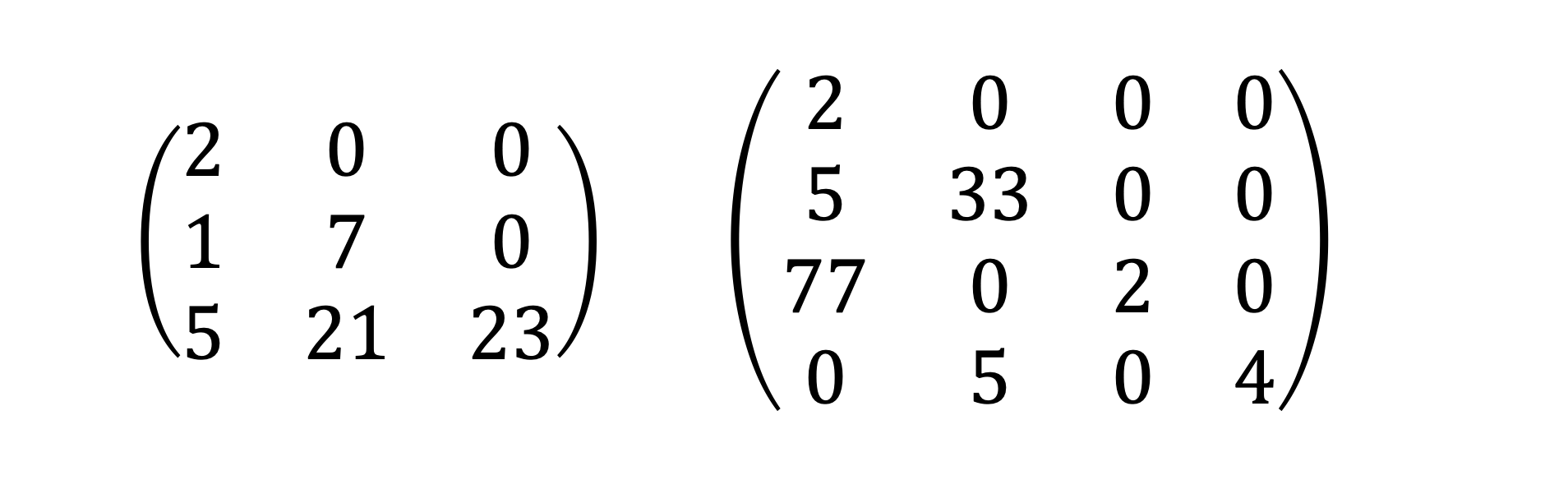
상삼각행렬
대각선 아래쪽이 모두 0인 행렬. 0이 아닌 원소가 있다면 주대각선과 대각선 위쪽 삼각에 있기 때문에 상삼각 행렬이라고 합니다.
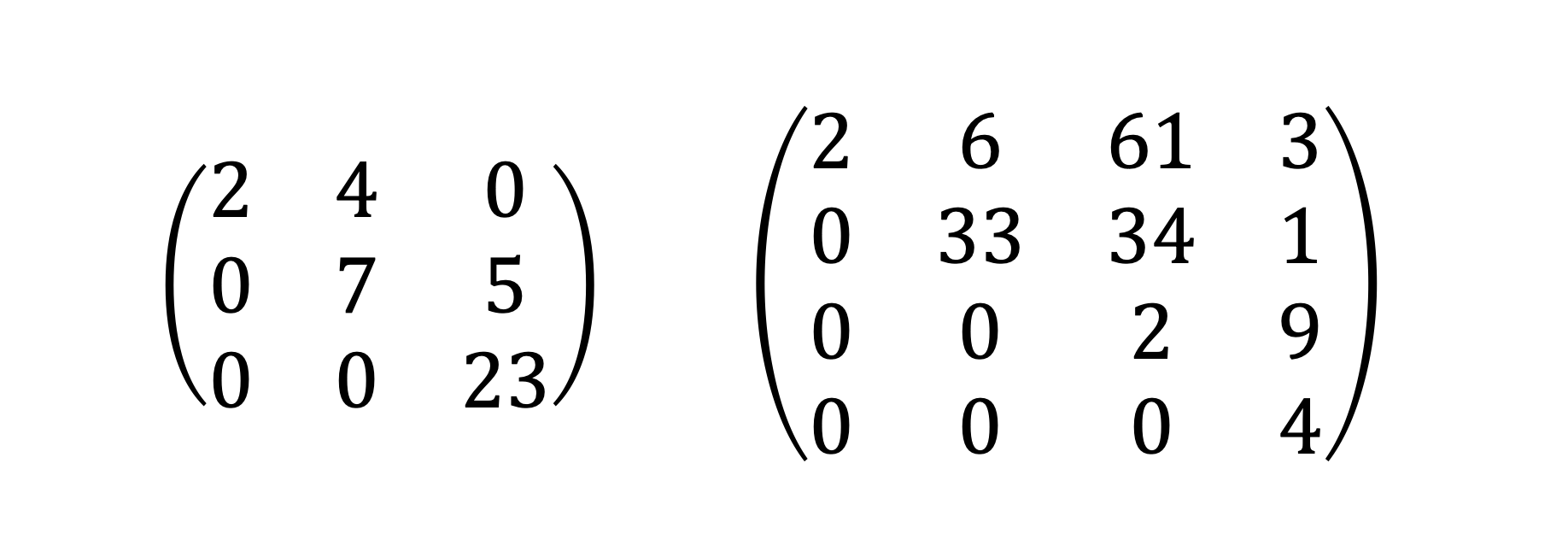
삼각행렬
하삼각행렬과 상삼각행렬을 묶어서 부르는 말.
스칼라행렬과 단위행렬
스칼라행렬
scalar matrix. 정방행렬 중 주대각원소의 값이 동일한 대각행렬.
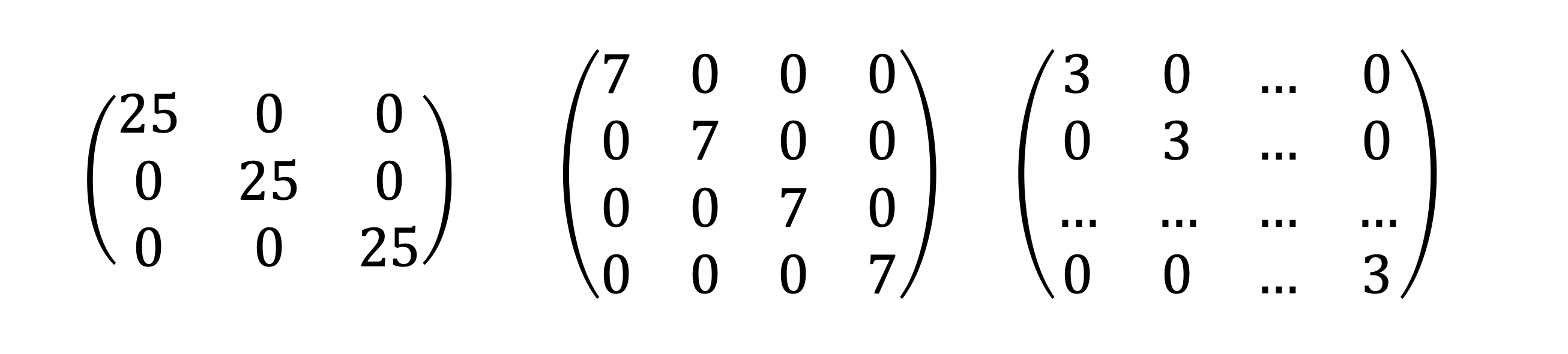
단위행렬
identity matrix. 정방행렬 중 주대각원소가 모두 1인 대각행렬.
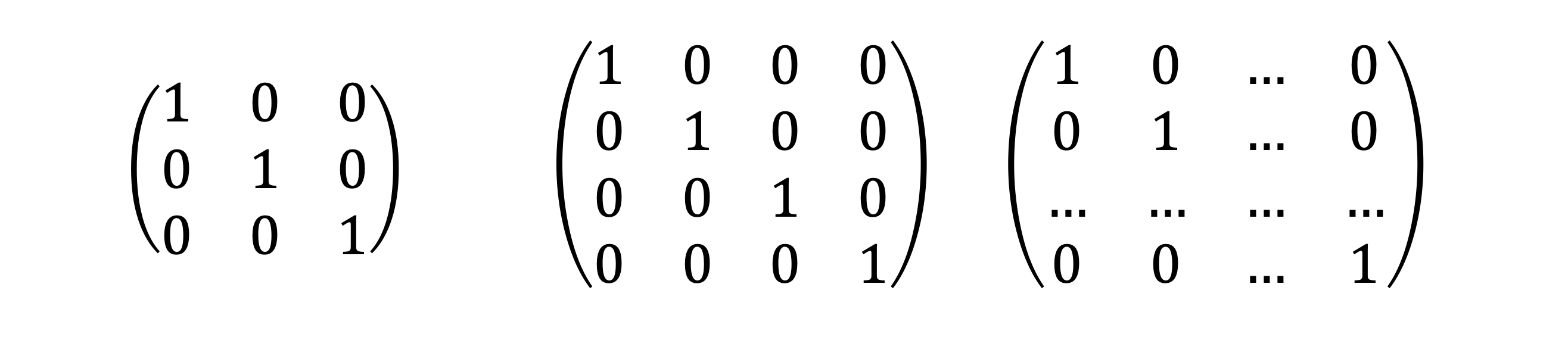
영행렬, 영행, 음행렬
영행렬
m x n 크기의 행렬 A에 대해 A + O = A 를 만족하는 행렬 O.
즉, 모든 원소가 0인 행렬을 뜻합니다.
영행
모든 원소가 0인 행.
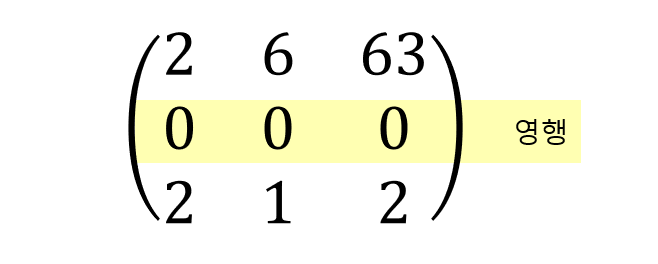
음행렬
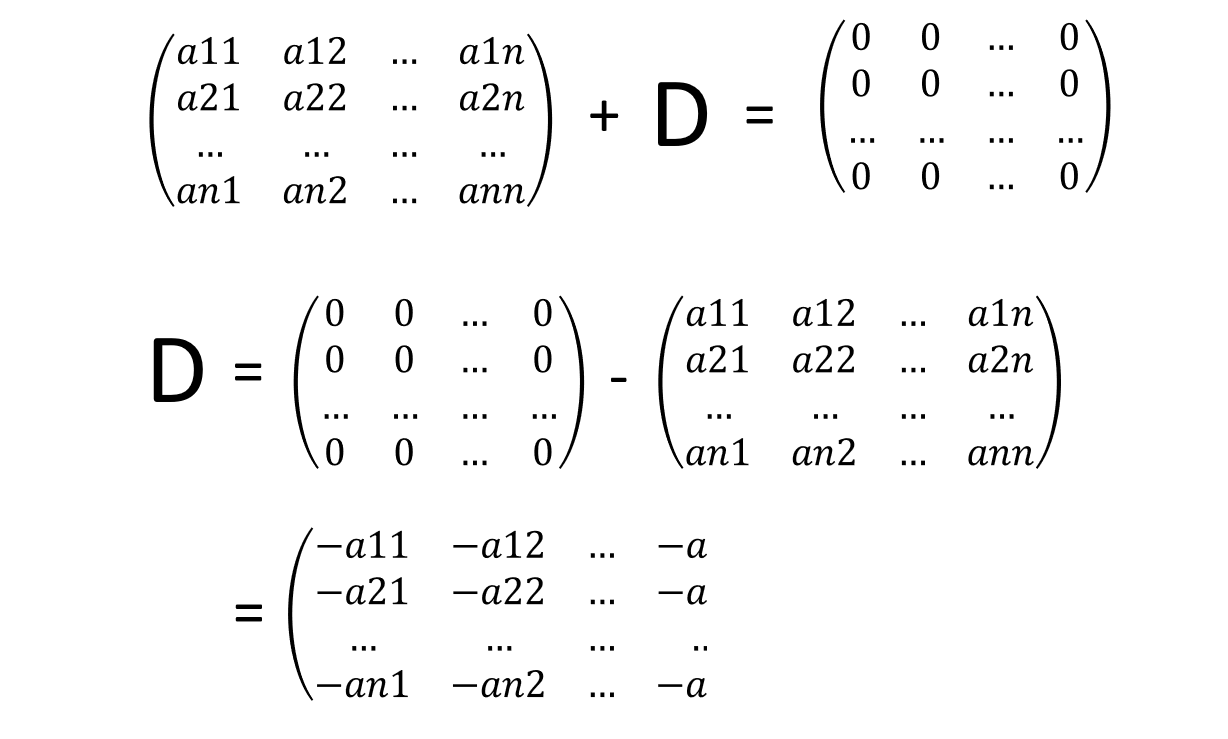
아래 두 가지 뜻으로 해석이 가능합니다.
(1) 행렬에 속한 모든 원소가 음수인 행렬
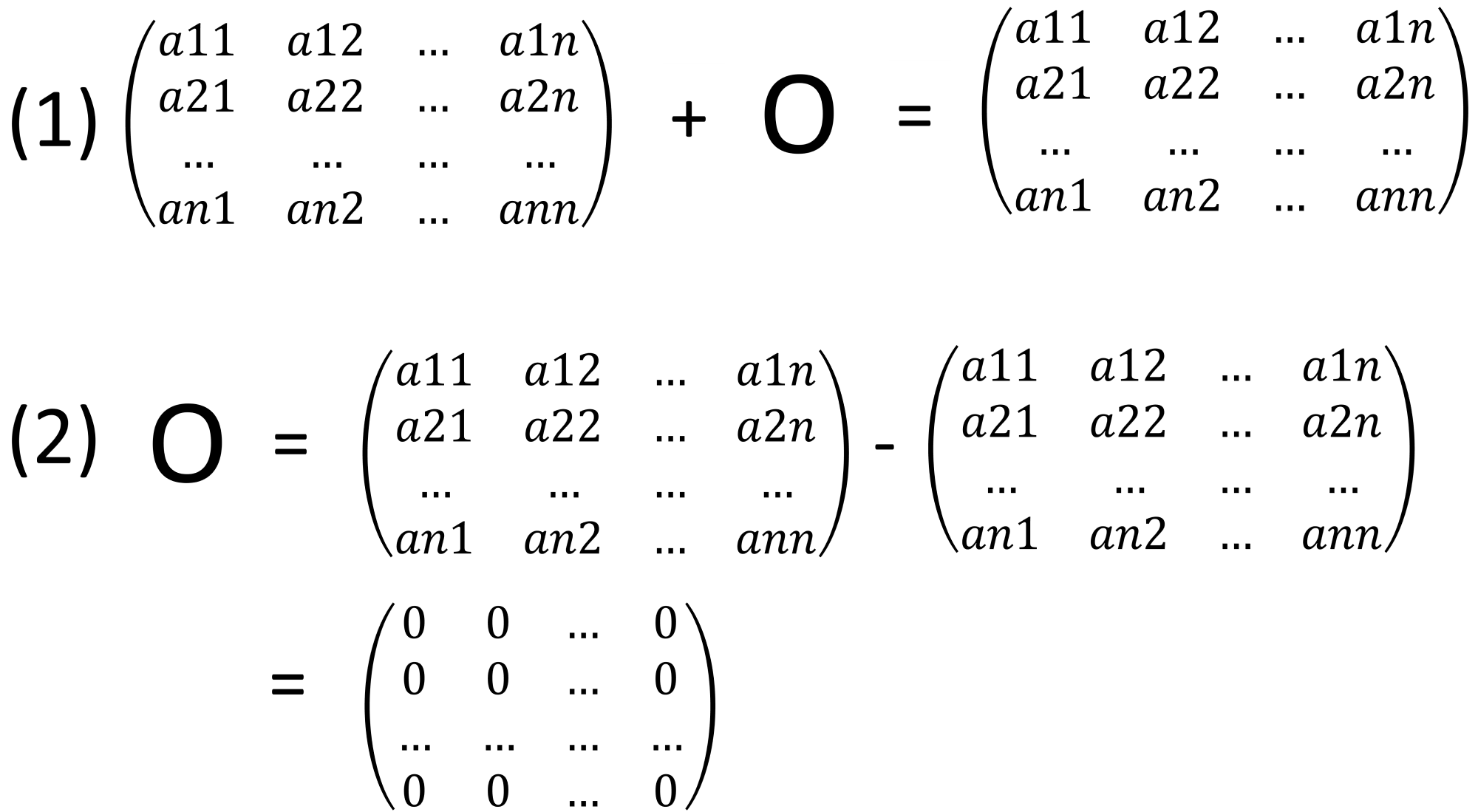
(2) A + D = O 를 만족하는 행렬 D = A의 음행렬
2번의 경우 아래와 같습니다.
전치행렬
행렬 A의 행과 열을 뒤집은 행렬을 행렬 A의 전치행렬 AT 라고 합니다.
정확하게 정의하자면, 행렬 A가 m x n 행렬이라고 할 때, A의 전치행렬 AT 는 n x m 행렬이며, A(i, j) = AT(j, i) 를 만족합니다.

대칭행렬과 비대칭행렬
대칭행렬
행렬 A와 A에 대한 전치행렬 AT 가 같은 행렬입니다. 즉, 주대각선을 기준으로 원소가 대칭되는 행렬입니다. 이를 위해서는 A는 정방행렬이어야 하며, A(i, j) = A(j, i) 를 만족해야 합니다.
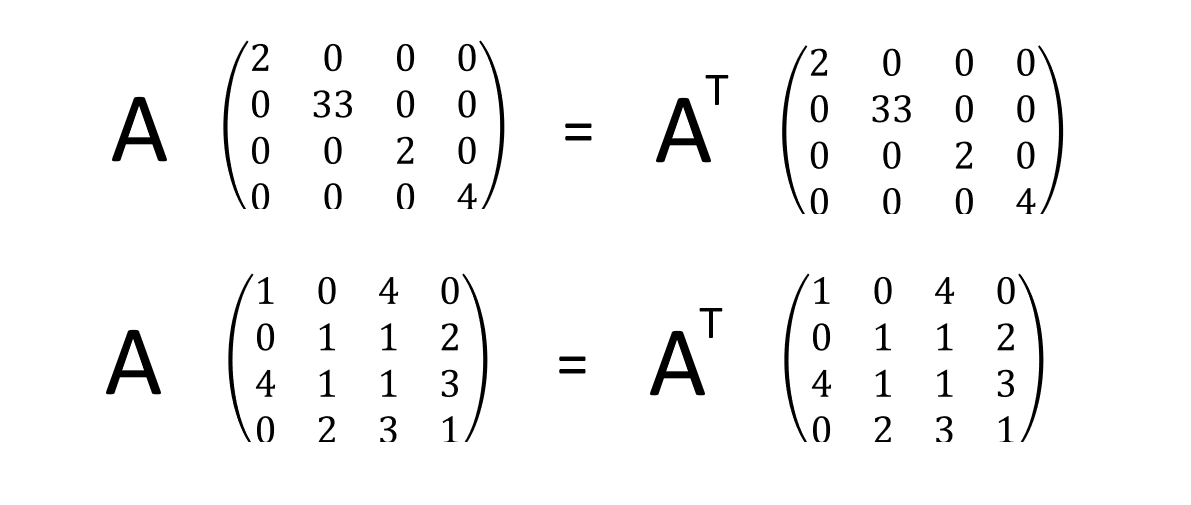
반대칭행렬 또는 비대칭행렬
행렬 A에 대해 전치행렬 AT = -A 를 만족하는 행렬을 반대칭행렬 또는 비대칭행렬이라고 합니다.
즉, 행렬 A의 모든 원소 A(i, j)에 대해 A(i, j) = -1 * AT(j, i).
(개인적인 의견으로는 반대칭행렬이 더 적합한 용어로 보임)
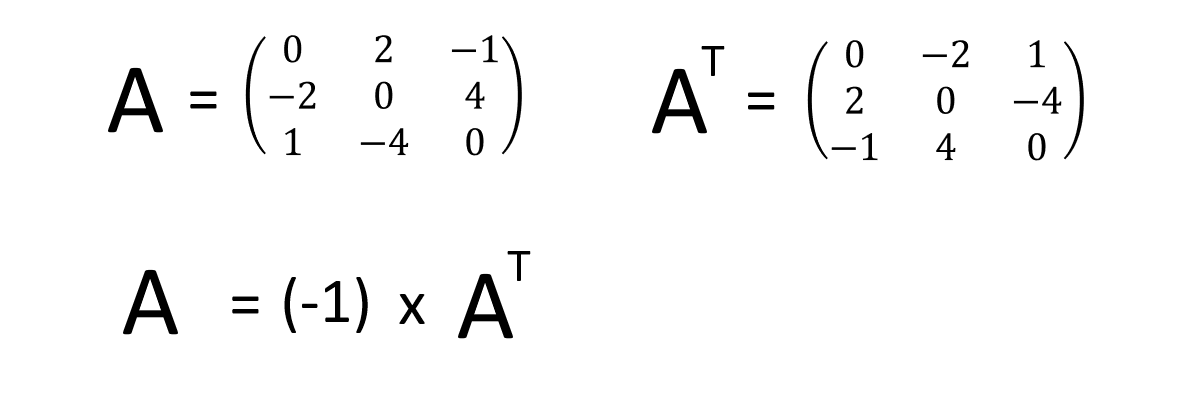

Comments