행렬 Matrix
행렬의 정의
In mathematics, a matrix is a rectangular array or table of numbers, symbols, or expressions, with elements or entries arranged in rows and columns, which is used to represent a mathematical object or property of such an object.
-wikipedia
즉, 행렬은 수 또는 다항식 등을 직사각형 모양으로 배열한 것입니다.
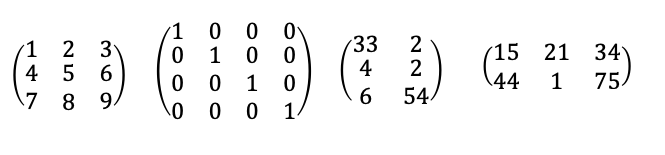
행과 열
행렬은 행과 열로 이루어져있습니다. 가로 방향으로 나열된 집합을 행, 세로 방향으로 나열된 집합을 열이라고 지칭합니다. 아래 예시와 같은 행렬에서 어떤 하나의 숫자는 각각 하나의 행과 하나의 열에 속하게 됩니다. 예를 들어 숫자 1은 1행과 1열에 속하고, 숫자 8은 3행과 2열에 속합니다.
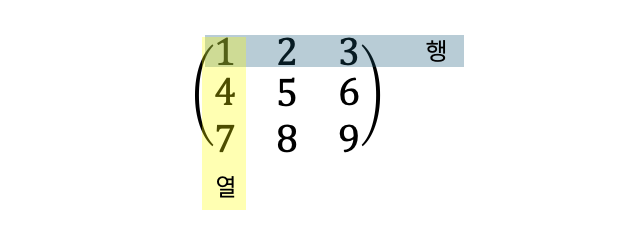
행렬의 크기
행렬의 크기는 행과 열의 개수로 표현됩니다. 3개의 행과 2개의 열을 가진 행렬은 3 X 2 행렬이라고 부르며, 이것을 일반화하면 m개의 행과 n개의 열을 가진 행렬의 크기는 m x n 이며, 이 행렬을 보통 m x n 행렬이라고 부르게 됩니다.
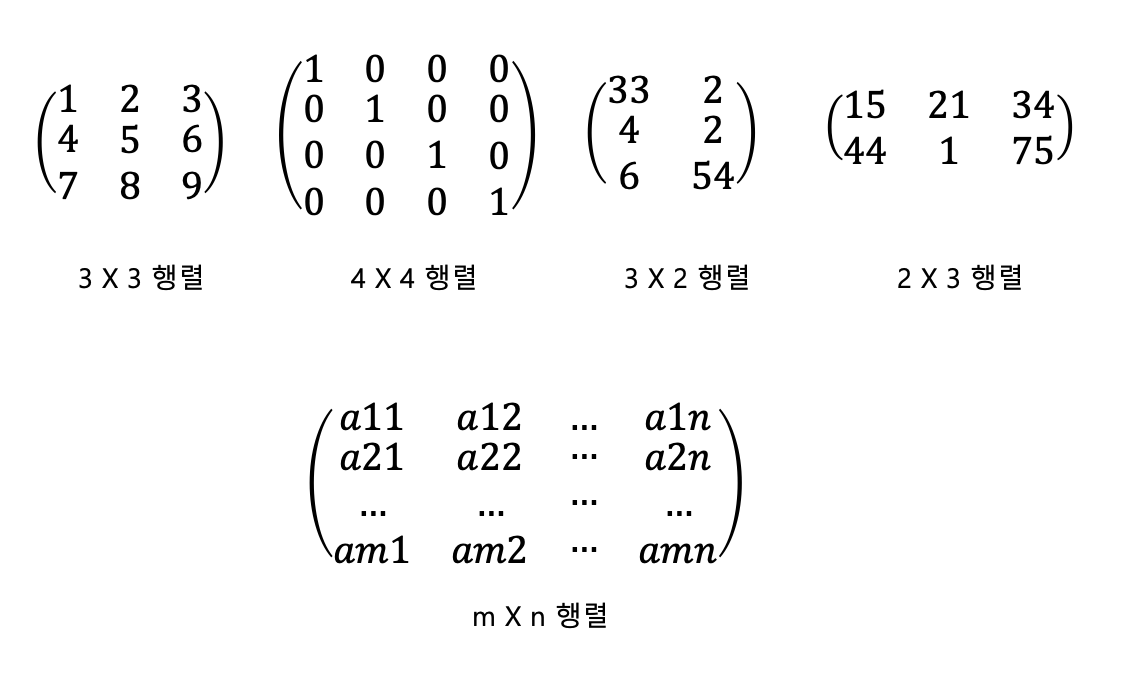
행렬의 원소 (성분)
행렬에 포함되는 각 값이나 수식 등은 원소 또는 성분이라고 지칭합니다. 아래 행렬에서는 1, 2, 3, 4, 5, 6, 7, 8, 9 가는 숫자 값을 가진 원소들이 포함되어있음을 볼 수 있습니다.
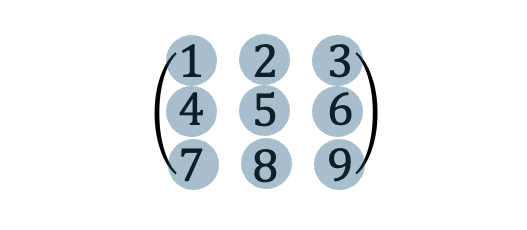
원소의 위치
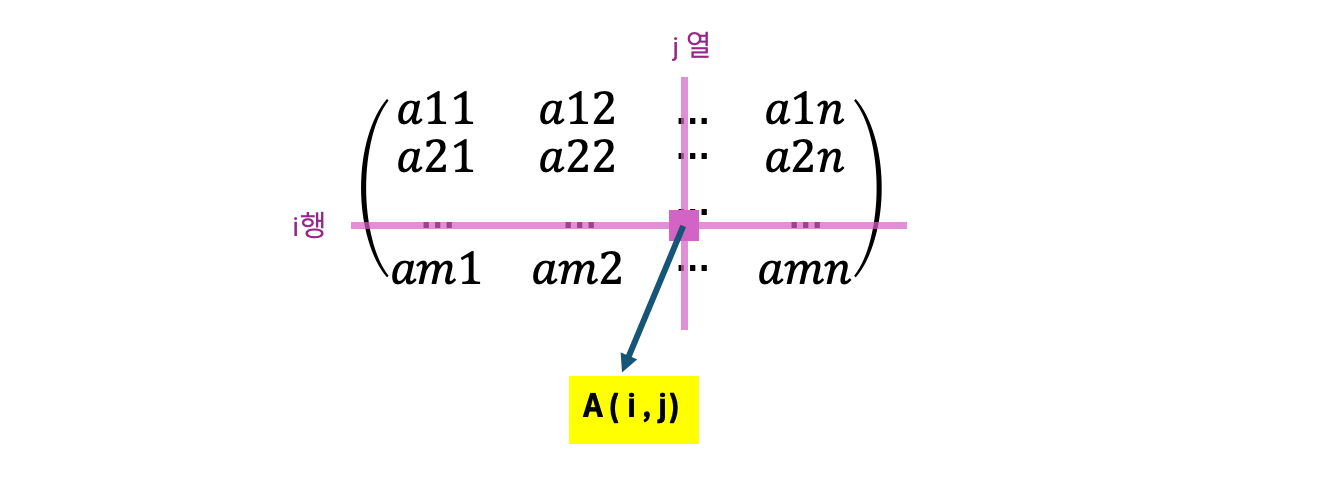
행렬 A에 속한 원소의 위치는 A(행번호, 열번호) 혹은 A[행번호, 열번호], A[행번호][열번호] 와 같이 표현할 수 있습니다. 마지막을 제외한 두 방식은 수학적으로 표현할 때 많이 사용되고, 마지막과 같이 대괄호 두개로 표현한 방식은 프로그래밍에서 행렬(2차 배열)에서 특정 위치의 원소값을 지칭할 때 많이 사용되는 방식입니다.
행렬을 왜 사용할까?
저는 수학을 좋아했습니다. 하지만 수학 중에서도 싫어했던 단원이 바로 행렬, 벡터, 그리고 확률과 통계 부분이었습니다. 그랬었는데 지금은 그것들이 가장 중요한 기본 개념으로 작동하는 컴퓨터 사이언스, 개발, 인공지능 분야에서 일을 하고 잇다는 것이 매우 아이러니 합니다.
제가 이들을 싫어했던 이유는 직관적이지 않고, 왜 이들을 공부해야 하는지 그 이유를 몰랐었기 때문입니다. 하지만 관련 분야에서 일을 하다보니, 행렬은 컴퓨팅에서 개념적으로, 혹은 연산의 기본 단위로 굉장히 많이 사용됨을 포착했습니다. 이번에는 행렬을 사용하는 이유에 대해 알아보겠습니다.
행렬의 등장 배경
행렬은 오랜 역사를 가진 수학적 개념으로, 기원전에도 연립방정식(여러 개의 선형 방정식)을 푸는 데 사용된 기록이 있습니다. 하지만 “행렬(Matrix)”라는 이름이 붙은 것은 1850년부터입니다. 행렬은 여러 개의 연립일차방정식을 체계적으로 푸는 방법을 고민하는 과정에서 발전되었습니다. 여러 미지수를 포함한 일차방정식 시스템을 쉽게 풀이하고 해의 존재 여부를 판단하기 위해, 방정식의 계수와 상수, 그리고 미지수를 분리하여 사용한 것이 바로 행렬의 시작입니다.
즉, 행렬은 등장 당시에는 자체로 의미가 있는 개념이라기보다는, 복잡한 연산을 간결하고 체계적으로 표현할 수 있는 도구로 주목받았습니다. 행렬을 통해 방정식들을 보다 효율적으로 다루고, 문제를 구조적으로 접근할 수 있었기 때문에, 수학적 문제 풀이에 큰 진전을 이룰 수 있었습니다.
현재는 이러한 초기의 목적을 넘어서 더 광범위한 의의를 가지게 되었습니다. 행렬은 선형대수학의 기초 개념으로서, 벡터 공간에서의 선형 변환을 간결하게 표현하는 도구로 발전했습니다. 또한, 물리학, 컴퓨터 그래픽스, 경제학, 통계학, 머신러닝 등 현대의 다양한 학문과 산업에서 핵심적인 역할을 하고 있습니다. 특히, 다차원 데이터를 구조적으로 다루고, 복잡한 계산을 효율적으로 처리할 수 있는 도구로서 행렬의 중요성은 더욱 커졌습니다. 현대 과학과 기술이 발전하면서, 행렬은 단순한 수학적 도구를 넘어 복잡한 시스템을 분석하고 최적화하는 필수적인 수단으로 자리 잡고 있습니다.
행렬을 사용하면 좋은 점
| 행렬의 장점 | 설명 |
|---|---|
| 계산 효율성 | - 행렬은 연립방정식을 간결하고 체계적으로 표현한 것 - 따라서 여러 방정식을 하나의 행렬로 나타낼 수 있음 - 행렬 연산(합, 곱 기본행렬 연산등) 및 가우스 소거법 등을 통해 - 여러 방정식을 한 번에 병렬적으로 처리 가능 |
| 대규모 데이터 처리 | - 위 계산 효율성과 동일함 - 현대에는 데이터가 많이 생성되고 있고, 이를 분석하는 빅데아터, 인공지능이 대두 - 이러한 분야들에서 대량의 데이터를 효율적으로 처리하기 위해 행렬이 필요 |
| 다차원 표현 | - 행렬은 여러 행, 열을 가지는 구조이기 때문에 다차원 자료를 표현하기 쉬움 - 특히 여러 개의 데이터를 체계적으로 정리하기가 쉬움(예: 이미지) - 또한 수학적으로 다차원에서의 위치값 혹은 벡터값 표기가 용이함 |
핵심은 여러 방정식의 계산에 있어 전통적인 방정식 풀이보다 효율적이고 빠른 계산이 가능하다는 점일 것입니다. 말로만 설명하면 이해가 어려울 수 있으니, 다음 포스트 들에서 행렬의 다양한 개념과 연산을 살펴보면서 행렬을 사용하면 좋은 점에 대해 느낄 수 있도록 공부해보겠습니다.


Comments