[ML] 스케일링(Scaling) - 정규화와 표준화 Normalization and Standardization

스케일링 (Scaling)

스케일 (Scale)

규모, 크기, 등급을 의미
측정이나 비교를 위한 기준, 즉 척도를 나타냄
음악에서는 특정 범위 내에서 표준화된 음계 체계를 의미함

스케일링 (Scaling)

서로 다른 단위나 범위를 공통된 척도로 맞추는 작업
비교나 연산을 공정하게 하기 위한 데이터 조정 과정

예시로 이해하기 (성적)

A 과목은 100점 만점, B 과목은 50점 만점이라고 가정해보자.
김철수는 A 과목에서 80점을, 박민수는 B 과목에서 45점을 받았다.
점수만 보면 판단이 어렵다. 만점 기준이 다르기 때문이다.
두 성적을 비교하려면 먼저 기준(만점)을 통일해야 한다.
예를 들어, 100점 만점 기준으로 환산하면 김철수는 80점, 박민수는 90점이다.
반대로 50점 만점 기준으로 보면 김철수는 40점, 박민수는 45점이다.
이렇게 점수를 같은 기준으로 맞춰 비교 가능하게 만드는 것이 스케일링이다.

예시로 이해하기 (요리)

1인분 기준의 파스타 레시피가 있다고 해보자.
이 레시피에는 면, 물, 소금, 올리브 오일, 마늘, 후추가 들어간다.
이제 4인분을 만들려면 어떻게 해야 할까?
모든 재료의 양을 4배로 동일하게 조정해야 한다.
이렇게 모든 항목을 동일한 비율로 조절하는 작업이 바로 스케일링이다.

특성 스케일링 (Feature Scaling)

정의

데이터의 범위를 조정하는 모든 기법을 통칭하는 포괄적 용어
데이터 처리 영역에서는 흔히 데이터 정규화라고도 불린다
데이터의 특징(피처) 또는 독립 변수들의 값을 동일한 척도(범위)로 변환하는 작업을 의미
스케일링의 핵심 목적은 여러 피처들의 값 범위를 비슷한 수준으로 조정하는 데 있다
단일 변수만 스케일링하고 나머지는 그대로 두는 것은 의미가 없다 — 모든 피처를 함께 조정해야 한다

스케일링이 필요한 이유

예를 들어 ‘키’와 ‘몸무게’라는 두 개의 피처가 있다고 가정해보자
키는 140~190cm, 몸무게는 40~100kg의 범위를 가진다고 해보면
몸무게의 값 범위가 더 넓기 때문에, 모델은 몸무게가 더 중요한 변수라고 잘못 판단할 수 있다
이 문제를 해결하려면, 키와 몸무게의 값을 같은 범위(또는 비슷한 크기) 로 맞춰야 한다
그렇게 하면 모델이 값의 크기 차이에 영향을 받지 않고
각 피처의 정보 중요도를 공정하게 판단할 수 있게 된다
이것이 바로 스케일링의 근본적인 목적이다

종류

종류	설명
정규화 Normalization	- 데이터의 값을 특정 범위 내로 변환하는 기법 - 스케일링의 한 종류
표준화 Standardization	- 데이터의 평균을 0, 표준편차를 1로 변환하는 기법 - 스케일링의 한 종류

정규화 Normalization

정의

서로 다른 척도로 측정된 값을 공통 척도로 조정하는 것
쉽게 말해 서로 다른 범위를 가진 두 개 이상의 피처를 동일한 특정 범위를 가지도록 변환하는 기법

예시

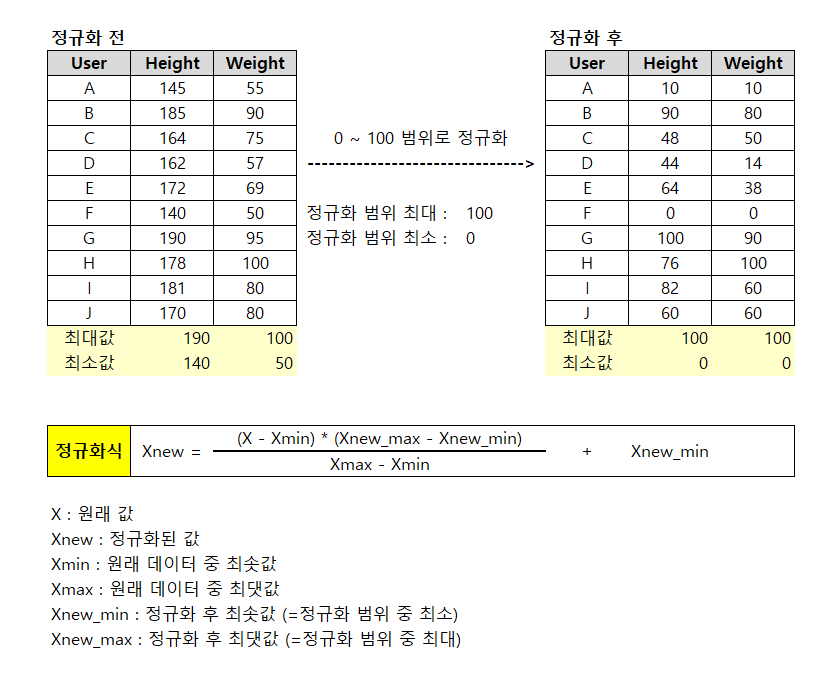
키는 140 ~ 190cm, 몸무게는 50 ~ 100kg 의 범위를 가진다고 가정한다.
이 두 피처에 속한 모든 데이터를 0~100 사이의 값으로 변환한다.

기법

기법	설명
최소-최대 스케일링 Min-Max scaling	최소 0 ~ 최대 1 사이의 값으로 정규화한다. 일반적인 정규화 방법
최대 절댓값 스케일링 MaxAbs scaling	-1 ~ 1 사이의 값으로 정규화한다. 즉, 절대값이 0 ~ 1 사이가 되도록 정규화한다.
로그 정규화 Log normalization	로그 변환을 통해 큰 값을 줄인다 또한 데이터 분포를 정규분포에 가깝게 만든다. 특히 지수적으로 퍼진 값에 적합하다.
평균 정규화 Mean normalization	데이터의 평균이 기준점(0)에 가깝게 한 뒤 -1 ~ 1 사이의 범위가 되도록 정규화를 하는 것
십진 스케일링 decimal scaling	데이터를 정규화해 -1 ~ 1 사이의 범위에 위치하도록 10 의 d 제곱으로 나누는 방법

최대 최소 스케일링 (Min-Max Scaling)

데이터를 최소 0 ~ 최대 1 사이의 값으로 정규화 하는 스케일링 기법.
일반적으로 정규화라고 하면 Min-Max scaling 을 가리킨다.

\[x_{\text{new}} = \frac{x - x_{\text{min}}}{x_{\text{max}} - x_{\text{min}}}\]

# Min Max Scaling
def custom_minmax_scaling(data:List[int]):
    x_max = max(data)
    x_min = min(data)
    result = [(x - x_min)/(x_max - x_min) for x in data]
    return result

data = [50, 90, 69, 80, 100]
scaled_data = custom_minmax_scaling(data)
print(scaled_data)

>> [0.0, 0.8, 0.38, 0.6, 1.0]

사이킷런의 MinMaxScaler 를 통해서 쉽게 사용할 수 있다.
이때는 2D Array 형태의 데이터를 집어넣어야 한다.

# Min Max Scaling
from sklearn.preprocessing import MinMaxScaler

data = [[50], [90], [69], [80], [100]]
scaler = MinMaxScaler()
scaled_data = scaler.fit_transform(data)
print(scaled_data.flatten())

>> [0.   0.8  0.38  0.6  1.  ]

최대 절댓값 스케일링 (MaxAbs Scaling)

-1 ~ 1 사이의 값으로 정규화한다. 즉, 절대값이 0 ~ 1 사이가 되도록 정규화 하는 것을 뜻한다.
데이터가 0을 중심으로 대칭적인 분포이거나, 음수와 양수가 섞인 데이터일 때 유용하다.
또한 희소행렬에서 특히나 효과적이다.

\[x_{\text{new}} = \frac{x}{|x_{\text{max}}|}\]

# MaxAbs scaling
data = [-100, 50, 90, 80, -40]
abs_max = max([abs(x) for x in data])
scaled_data = [x/abs_max for x in data]
print(scaled_data)

>> [-1.0, 0.5, 0.9, 0.8, -0.4]

사이킷런의 MaxAbsScaler 를 사용해서 쉽게 사용할 수 있다.
이때는 2D Array 형태의 데이터를 집어넣어야 한다.

# MaxAbs scaling
from sklearn.preprocessing import MaxAbsScaler

data = [[-100], [50], [90], [80], [-40]]
scaler = MaxAbsScaler()
scaled_data = scaler.fit_transform(data)
print(scaled_data.flatten())

>> [-1.   0.5  0.9  0.8 -0.4]

로그 정규화 (Log Normalization)

로그 변환을 통해 큰 값을 줄이고, 데이터 분포를 정규분포에 가깝게 만든다.
특히 지수적으로 커지는 데이터나 오른쪽으로 치우친 분포(positive skew)에 효과적이다.

\[x_{\text{new}} = \log(x + c)\]

c : 상수로 보통 1을 사용한다. log 를 취한 값이 0이나 음수가 되는 것을 방지하기 위해 사용한다.

from math import log

data = [81, 243, 729, 2187]
scaled_data = [log(x) for x in data]
print(scaled_data)

>> [4.394449154672439, 5.493061443340548, 6.591673732008658, 7.690286020676768]

평균 정규화 (Mean Normalization)

데이터의 평균을 기준점(0)에 놓고, 데이터가 -1 ~ 1 사이의 범위가 되도록 정규화를 하는 것
결과적으로 정규화된 값들은 -1 ~ 1 사이로 분포하며, 중심은 0에 가까워진다.
쉽게 말해, 값에 평균값을 뺀 뒤, 데이터의 최대 최소값의 차이로 나누는 것이다.
일반적으로 MinMaxScaler 나 MaxAbsScaler 보다 성능 개선효과가 크지 않아 잘 쓰이지 않음

\[x_{\text{new}} = \frac{x - x_{mean}}{x_{max} - x_{min}}\]

# mean normalization
data = [-100, -90, -50, -40, 25, 25]
x_mean = sum(data)/len(data)
x_max = max(data)
x_min = min(data)
scaled_data = [(x - x_mean)/(x_max - x_min) for x in data]
print(scaled_data)

>> [-0.4933.., -0.4133.., -0.0933.., -0.0133.., 0.5066.., 0.50666..]

십진 스케일링 (Decimal Scaling)

데이터를 정규화해 -1 ~ 1 사이의 범위에 위치하도록 10 의 d 제곱으로 나누는 방법

\[x_{\text{new}} = \frac{x}{10^d}\]

# decimal scaling
from math import pow

data = [-10230, 48273, 1836, 28462, -100000]
d = len(str(max([abs(x) for x in data]))) - 1
scaled_data = [x/pow(10, d) for x in data]
print(scaled_data)

>> [-0.1023, 0.48273, 0.01836, 0.28462, -1.0]

정규화를 해야할 때는?

적용 상황	설명
특징들의 범위가 크게 다를 때	예: 키(cm)는 150~200, 수입은 0~10,000,000 → 모델이 큰 값에 쏠릴 수 있음
거리 기반 알고리즘을 사용할 때	예: K-NN, K-Means, SVM (RBF 커널 등) → 피처 간 거리 계산이 핵심이므로 스케일 통일이 중요
신경망 모델에 사용할 때	활성화 함수가 민감하게 작동 → 입력을 0~1 또는 -1~1로 맞춰줘야 성능 안정
음수와 양수의 위치성을 유지하고 싶을 때	정규화를 통해 상대적인 위치 유지 가능

장단점

장점 : 모든 데이터의 범위를 통일시키므로 비교하기 편함
단점 : 이상치에 민감. 이상치가 존재하면 정상 데이터가 한쪽으로 쏠려 모델 성능이 떨어질 수 있음.

표준화 Standardization

정의

개별 피처(특성)의 평균을 0, 표준편차를 1로 변환하는 기법
데이터의 분포를 가우시안 정규분포 형태로 만드는 것을 표준화라고 한다.
여러 모델들은 입력 데이터를 평균 0, 그리고 동일 차수의 분산을 갖는다고 가정할 수 있으므로 표준화 작업은 모델 성능 측면에서 매우 중요하다.

예시

💡 상황:
학생 A: 수학 85점, 체육 70점
학생 B: 수학 65점, 체육 90점

단순 평균으로 평가하면?
A 평균: (85 + 70) / 2 = 77.5
B 평균: (65 + 90) / 2 = 77.5
👉 두 학생의 점수가 같아 보임

☝️ 그런데…
수학은 전체 평균이 60점, 표준편차가 15점
체육은 전체 평균이 90점, 표준편차가 5점
→ 수학은 어려운 과목, 체육은 다 잘 보는 과목

🔎 표준화(Z-score)로 바꿔보면?

A의 수학 Z = (85 - 60)/15 = 1.67
A의 체육 Z = (70 - 90)/5 = -4.00
평균 Z = (1.67 + -4.00) / 2 = -1.165

B의 수학 Z = (65 - 60)/15 = 0.33
B’s 체육 Z = (90 - 90)/5 = 0.00
평균 Z = (0.33 + 0.00) / 2 = 0.165

😳 차이점:
단순 점수 기준 → 두 학생이 똑같이 잘했다
표준화 기준 → B가 더 우수한 성취
과목 난이도와 분포를 반영하니, 겉보기 점수와 완전히 다른 판단 결과가 나옴

기법

기법	설명
Z-score 표준화 Standard scaling	- 평균 0, 표준편차 1로 스케일링 - 이상치에 다소 민감
중앙값 기준 표준화 Robuster scaling	- 이상치에 강건함 - 데이터의 분포를 크게 왜곡하지 않음

Z-score 표준화 (Standart Scaling)

데이터의 평균(μ) 을 0으로, 표준편차(σ) 를 1로 맞추는 스케일링 방법.
데이터가 정규분포를 따른다고 가정할 때 가장 적합하다.
이상치(outlier) 에 다소 민감하여, 왜곡이 생길 수가 있다. (평균과 표준편차가 이상치에 영향을 받기 때문)

\[x_{\text{new}} = \frac{x - x_{\text{mean}}}{\sigma}\]

# standard scaling
data = [10, 20, 30, 40, 50]
mean = sum(data) / len(data)
std = (sum((x - mean) ** 2 for x in data) / len(data)) ** 0.5
z_score_scaled = [(x - mean) / std for x in data]
print(z_score_scaled)

>> [-1.414213562373095, -0.7071067811865475, 0.0, 0.7071067811865475, 1.414213562373095]

사이킷런의 StandardScaler를 이용하면 쉽게 사용할 수 있다.

# standard scaling
from sklearn.preprocessing import StandardScaler
import numpy as np

data = np.array([[10], [20], [30], [40], [50]])
scaler = StandardScaler()
z_score_scaled = scaler.fit_transform(data)
print(z_score_scaled.flatten())
>> [-1.41421356 -0.70710678  0.   0.70710678  1.41421356]

중앙값 기준 표준화 (Robust Scaling)

데이터의 중앙값(median) 을 기준으로 데이터를 중심화하고, 사분위 범위(IQR = Q3 - Q1) 로 나누어 스케일링하는 기법
이상치에 강건함 (평균이나 표준편차 대신 중앙값과 IQR을 쓰기 때문)
데이터가 비대칭, 이상치 포함 분포를 가질 때 적용하기 적합하다.
데이터의 분포를 크게 왜곡하지 않으면서 스케일 조정이 가능하다.
이게 단점일 수도 있는데, 분포의 형태가 많이 보존되어 모델에 따라 오히려 불리할 수도 있음.

\[x' = \frac{x - {x_{\text{median}}}}{\text{IQR}}\]

# Robust Scaling
import numpy as np

data = [10, 20, 30, 40, 100]  # 이상치 포함

# 중앙값과 IQR 계산
q1 = np.percentile(data, 25)
q3 = np.percentile(data, 75)
median = np.median(data)
iqr = q3 - q1

# Robust 표준화
robust_scaled = [float((x - median) / iqr) for x in data]
print(robust_scaled)

>> [-1.0, -0.5, 0.0, 0.5, 3.5]

사이킷런의 RobustScaler 를 이용하면 더 쉽게 사용할 수 있다.

# Robust Scaling
from sklearn.preprocessing import RobustScaler

data = np.array([[10], [20], [30], [40], [100]])

scaler = RobustScaler()
robust_scaled = scaler.fit_transform(data)

print(robust_scaled.flatten())

>> [-1.  -0.5  0.   0.5  3.5]

표준화를 해야할 때는?

적용 상황	설명
피처들의 단위·범위가 제각각일 때	예: 키(cm) vs 체중(kg) vs 수입(₩) → 표준화를 통해 단위의 영향 제거 및 가중치 비교 가능
분산 기반 알고리즘을 사용할 때	선형회귀, 로지스틱회귀, 선형SVM선형, PCA, kmeans 등 → 평균과 표준편차 기준 스케일링이 모델 가정에 부합
정규분포/근사 분포를 가정하는 경우	예: 의료 데이터, 시험 점수 등 → 평균 0, 표준편차 1로 조정 시 모델 성능 향상 가능
이상치는 적지만 값의 분포가 넓을 때	Robust Scaler가 필요할 정도는 아니지만 범위 차이가 커서 특정 피처가 주도하게 되는 경우

장단점

장점 : 이상치의 영향을 덜 받는다. 이상치가 있어도 데이터 분포 형태가 크게 왜곡되지 않음
단점 : 정규화와 달리 데이터 최소, 최대값이 정해져 있지 않아, 데이터의 범위가 계속 바뀔 수 있다.

Reference

https://scikit-learn.org/stable/modules/preprocessing.html#standardization-or-mean-removal-and-variance-scaling
https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MinMaxScaler.html#sklearn.preprocessing.MinMaxScaler
https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MaxAbsScaler.html#sklearn.preprocessing.MaxAbsScaler
https://www.etymonline.com/search?q=scale
https://en.wikipedia.org/wiki/Feature_scaling
https://www.datacamp.com/tutorial/normalization-vs-standardization
이기적 데이터 분석기사

Twitter Facebook LinkedIn

[ML] 스케일링(Scaling) - 정규화와 표준화 Normalization and Standardization

Jongya

스케일링 (Scaling)

스케일 (Scale)

스케일링 (Scaling)

예시로 이해하기 (성적)

예시로 이해하기 (요리)

특성 스케일링 (Feature Scaling)

정의

스케일링이 필요한 이유

종류

정규화 Normalization

정의

예시

기법

최대 최소 스케일링 (Min-Max Scaling)

최대 절댓값 스케일링 (MaxAbs Scaling)

로그 정규화 (Log Normalization)

평균 정규화 (Mean Normalization)

십진 스케일링 (Decimal Scaling)

정규화를 해야할 때는?

장단점

표준화 Standardization

정의

예시

기법

Z-score 표준화 (Standart Scaling)

중앙값 기준 표준화 (Robust Scaling)

표준화를 해야할 때는?

장단점

Reference

Comments

You May Also Enjoy

20250808_001_system_engineering_life_cycle

업스트림(Upstream)과 다운스트림(Downstream)

사일로 현상 (silo effect)

내 수학적 직관은?(유튜브 임커밋 컨텐츠 리뷰)