내 수학적 직관은?(유튜브 임커밋 컨텐츠 리뷰)

문제

• 앞면과 뒷면이 있는 동전이 있다.
• 앞면은 빨간색, 뒷면은 파란색이다.

• 이런 동전이 100개가 놓여있다.

• 이 중 무작위로 10개의 동전을 뒤집는다.

• 그리고 흑백 안경을 써서 앞면과 뒷면 색이 구분되지 않게 한다.
• 이후 동전의 순서를 무작위로 뒤섞는다.

• 100개 중 10개의 동전을 뽑는다.
• 여기서 문제
• 뽑힌 동전 그룹(SELECTED)과 남은 동전 그룹의 뒷면(파란색) 개수를 동일하게 만들려고 한다.
• 동일하게 맞추기 위해 동전을 이동하거나, 뒤집을 수 있다.
• 어떻게 하면 두 그룹의 뒷면 개수를 동일하게 만들 수 있을까?

정답

정답 펼치기/접기

정답

• 뽑힌 그룹(SELECTED)의 동전을 모두 한 번씩 뒤집으면 된다.

해설

• 수식으로 표현을 해보면 쉽게 이해할 수 있다.
• SELECTED 그룹에 포함된 뒷면(파란색) 동전의 개수를 X 개라고 해보자.
• 두 그룹을 합친 100개의 동전 중 뒷면(파란색) 동전의 개수는 총 10개이고
• 그렇다면 나머지 그룹의 뒷면(파란색) 동전의 개수는 (10 - X)개가 된다.
• 여기서 SELECTED 그룹의 모든 동전을 뒤집으면 10 - X 개가 되므로 두 그룹의 뒷면 동전의 개수는 동일하게 된다.

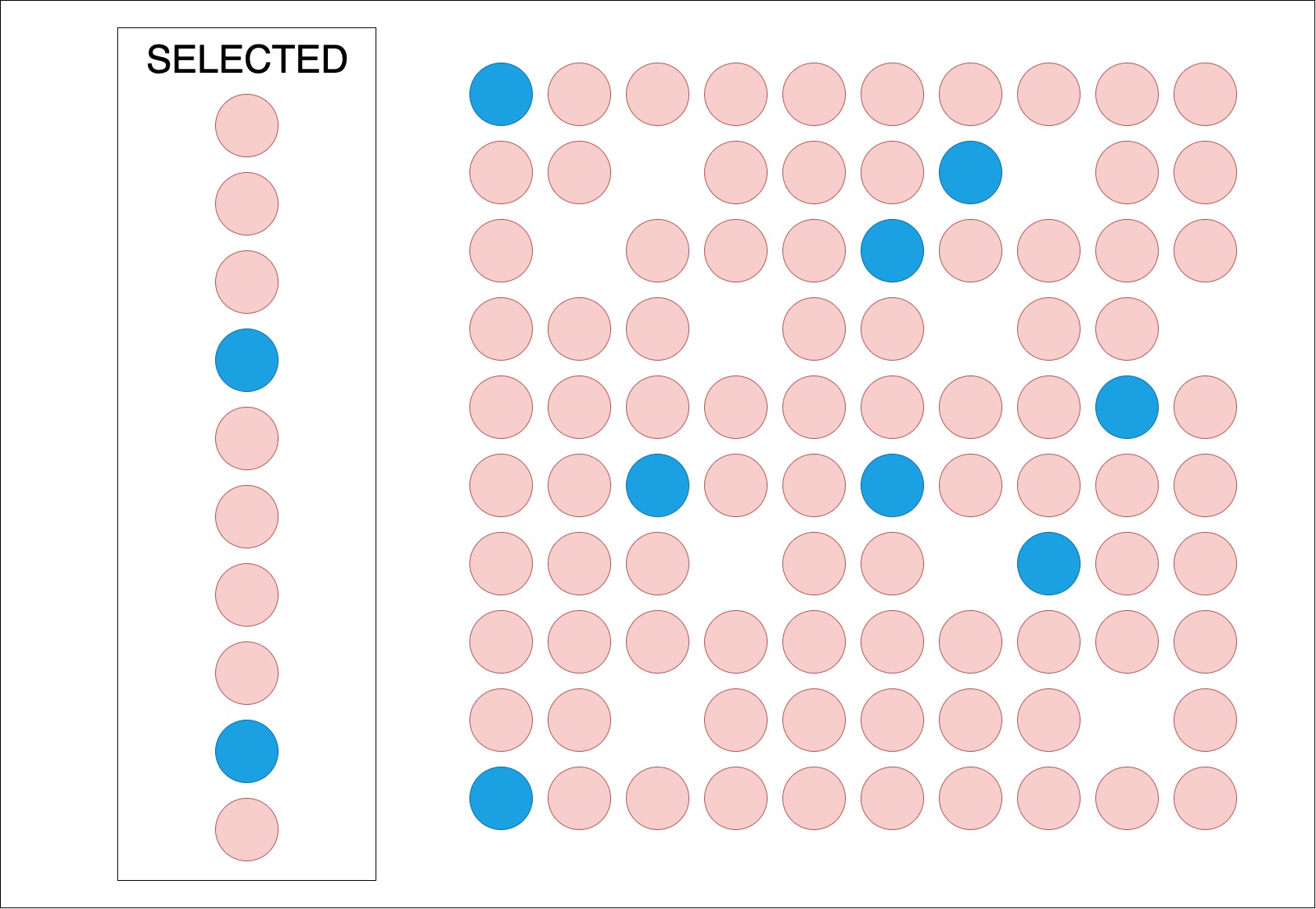
• 흑백 안경을 벗어보면 위와 같은 그림일 것이다.
• 여기서 SELECTED 그룹의 뒷면 동전의 개수 X=2개
• 나머지 그룹의 뒷면 동전은 (10 - 2) = 8개가 된다.

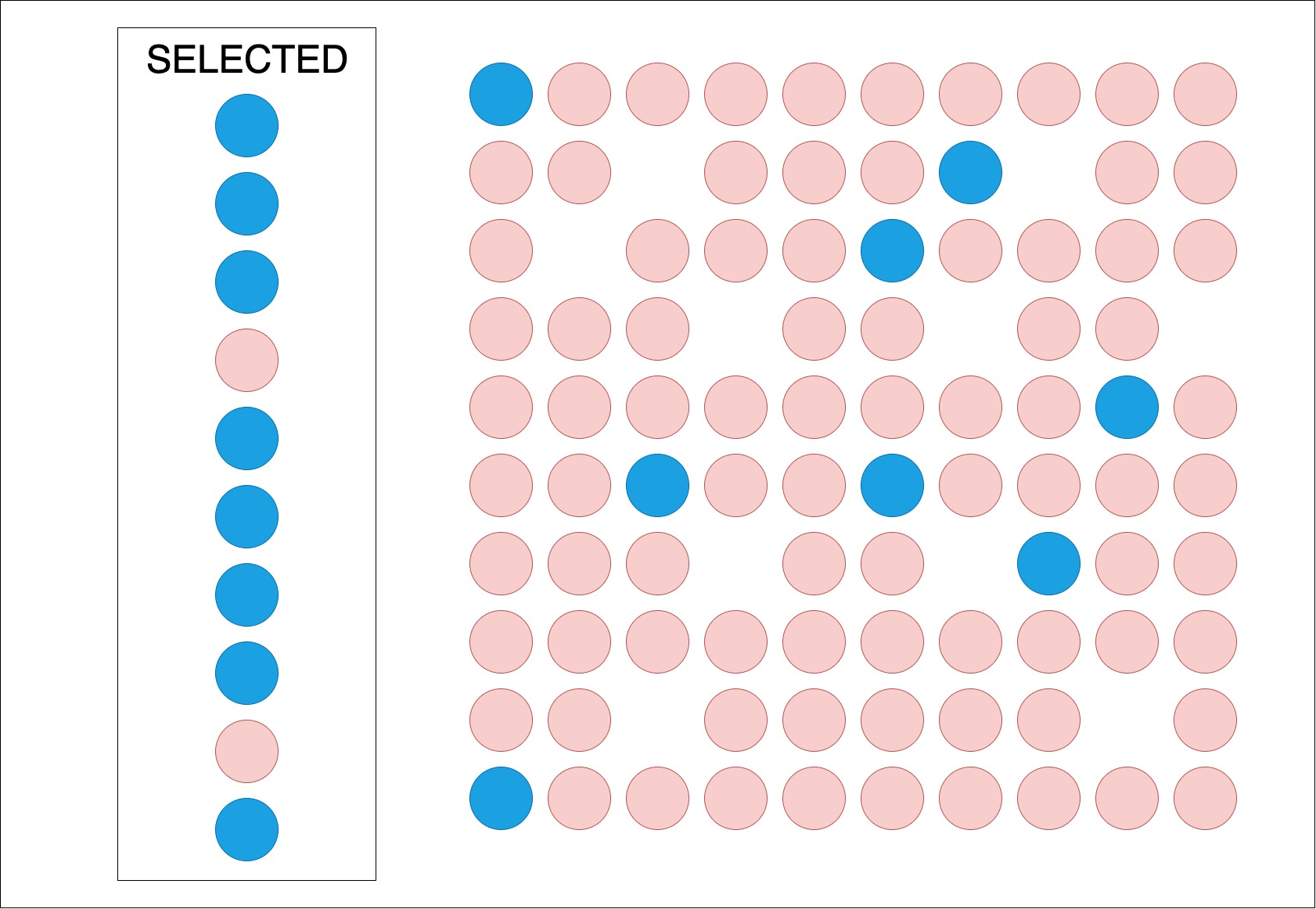
• SELECTED 그룹의 모든 동전을 뒤집으면
• SELECTED 그룹의 뒷면 동전은 10 - X = 8개가 된다. (X=2)
• 그러면 두 그룹의 뒷면 동전은 8개로 동일!

리뷰

• 문제만 보고 풀지 못해서 정답을 봤다.
• 이러한 수학적 문제를 수식으로 표현해보면 생각보다 쉽게 풀린다는 것을 깨달음

Reference

임커밋 - 내 수학적 직관은?