이산수학
이산수학이란
이산적인 수학구조에 대해서 연구하는 학문으로 연속되지 않는 공간을 다룬다.
이산적인 것과 반대되는 것은 바로 “연속적인” 것으로, “실수값”을 대표적으로 꼽을 수 있다.
이산적이라는 것을 설명하자면 “서로 구분되는” 혹은 “셀 수 있는” 정도로 설명할 수 있을 것이다.
| 영문명칭 | 분리 | 어원 |
|---|---|---|
| discrete mathematics | dis- | 떨어져있는(separate) |
| cernere | 구별하다(to distinguish) |
| 한자어 | 뜻 |
|---|---|
| 離 | 떠날 리. 떠나다, 떼어놓다, 따로 떨어지다. |
| 散 | 흩을 산. 흩다. 흩어지다. 헤어지다. 풀어놓다. 한가하다. |
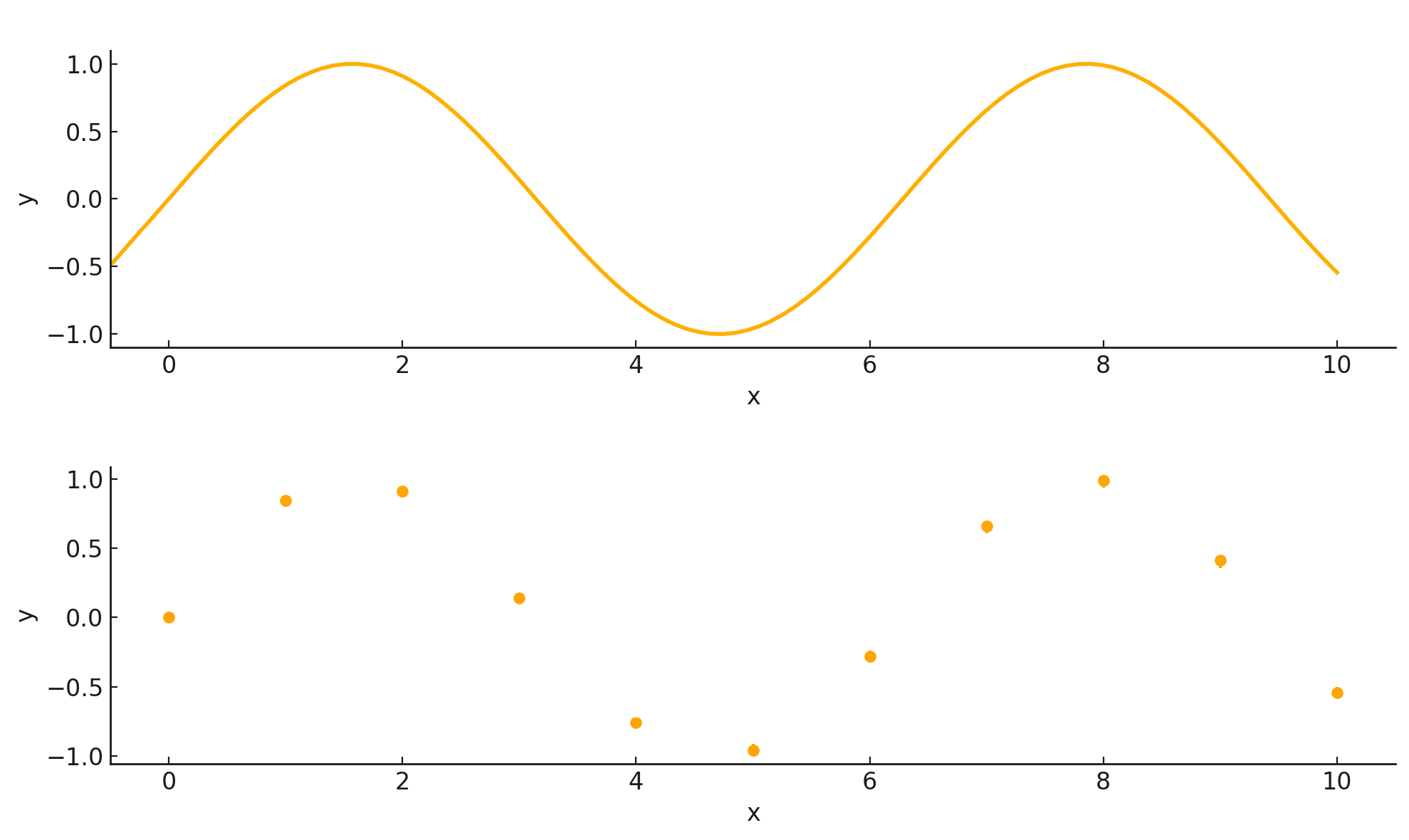
이산적인 값과 연속적인 값
이산수학에서 다루는 주제와 응용 분야
| 이산수학의 주제 | 컴퓨터 응용 분야 |
|---|---|
| 논리 | 전문가 시스템 |
| 증명 | 컴퓨터 프로그램의 효과성 및 효율성 입증 |
| 집합론 | 계산 이론, 데이터베이스 등 |
| 행렬 | 2차원 그래픽, 3차원 그래픽, 기계학습(AI) |
| 관계 | 관계형 데이터베이스 |
| 함수 | 컴퓨터 언어 |
| 부울대수 | 계산 이론, 디지털 논리회로 |
| 그래프 | 자연어 처리, 컴퓨터 네트워크 |
| 트리 | 자료 탐색, 컴퓨터 네트워크, 데이터베이스, 회로망 설계 |
| 조합이론 | 계산 이론 |
| 정수론 | 정보 보안 |
| 오토마타 및 형식 언어 | 계산 이론, 문제 해결 가능성 |
물론 이산수학의 특정 주제가 위의 표와 같은 응용 분야와만 딱 관계가 있는 것은 아니다. 더 많은 분야들과 관계가 있지만, 대표적으로 꼽자면 위의 표와 같은 것이다.
더불어, 시간이 흐르면서 응용 분야가 바뀌는 경우도 있다. 예를 들어 행렬은 AI 붐 이전까지 그래픽 관련 컴퓨팅에서 자주 사용되었지만, 지금은 AI와 컴퓨터 학습에서 데이터 혹은 연산의 단위로 굉장히 중요하게 사용되고 있다.

Comments