데이터베이스 모델링 (3) 개념적 데이터 모델링과 ER 모델

개념적 데이터 모델링

개념적 데이터 모델링의 개념

사용자의 요구사항을 바탕으로 데이터베이스 모델링에 진입하고, 프로그램 개발에 들어가기 앞서 요구사항이 잘못 해석되는 오류를 피하기 위한 추상화 단계이다. 쉽게 말해 비즈니스 요구사항을 반영해 데이터의 전반적인 구조와 관계를 정의하는 즉, 청사진을 그리는 단계이다.

이러한 개념적 데이터 모델링은 실세계의 데이터들을 개념적으로 일반화시키면서 이들의 데이터타입, 속성, 관계, 제약조건들을 뽑아내고 이것을 의사소통에 쓰일 수 있게끔 시각화 하거나 명세하는 작업까지 포함한다.

현재까지 제안된 개념적 데이터 모델은 객체 모델, 시멘틱 네트워크 모델, ER 모델 등이 있으며 가장 대표적으로 활용되는 것은 ER 모델이다.

ER 모델

ER 모델의 개념

ER 모델의 ER 은 각각 Entity 와 Relationship을 뜻하며, 데이터를 엔티티(Entity)와 그들 간의 관계(Relationship)로 표현하여 실세계의 업무의 의미와 상호 작용을 개념적으로 나타내는 데 유용하게 활용되고 있다.

1976년 첸 박사가 제안한 모델로, 현재 가장 대표적인 개념적 데이터 모델링 기법이다.

Entity 와 Relationship

구성요소	영문 명칭	설명
개체	entity	- 데이터로 관리하려는 각각의 개별적인 유무형의 개체 또는 개념 을 지칭한다. - 개체는 개체를 설명하는 여러 속성들로 구성된다.
개체 집합	entity set	- 동일한 속성의 유형을 공유하는 개체들의 모임이다.
관계	relationship	- 한 개체와 다른 개체가 서로 어떤 관계인지 연관성을 지칭하는 말이다.
관계 인스턴스	relationship instance	- 관계 중 특정한 하나의 관계
관계 집합	relationship set	- 한 개체 집합과 다른 개체 집합간의 관계를 뜻한다.
속성	attribute	- 개체 혹은 개체 집합이 가지는 특성이며, 값을 가진다. (1) 더 작은 요소로 나눌 수 있는지에 따라 단순 속성과 복합 속성으로 나뉨 (2) 개체당 가질 수 있는 개수에 따라 단일값 속성과 다중값 속성으로 나뉨 (3) 유추할 수 있는지 여부에 따라 유도 속성과 저장 속성으로 나뉨
제약조건	constraints	- 데이터(엔티티, 릴레이션)가 준수해야 하는 규칙을 지칭함. (1) 사상수 (2) 참가 제약조건 (3) 키 속성

ER 모델의 구성요소

개체와 개체집합

개체란 데이터로 관리하려는 각각의 개별적인 유무형의 개체 또는 개념 을 지칭한다. 개체는 개체를 설명하는 여러 속성들로 구성된다.

개체 집합이란 동일한 속성의 유형을 공유하는 개체들의 모임이다.

개체 집합 구분	설명
약한 개체 집합	개체 집합의 존재 유무가 관계를 맺고 있는 개체의 존재에 종속되는 개체 집합
강한 개체 집합	약한 개체 집합과 연결되는 일반 개체 집합. 즉, 상대 개체의 존재 유무를 결정하는 개체 집합

예시
-학번은 1234이고, 이름은 홍길동이며, 3학년인 사람 -> 개체
-학번, 이름, 학년 이라는 속성을 가진 ‘학생’들의 집합 -> 개체 집합
-계좌(계좌 개체 집합)를 소유한 학생(학생 개체 집합) -> 강한 개체(개체 집합)
-학생(학생 개체 집합) 에게 소유되는 계좌(계좌 개체 집합) -> 약한 개체(개체 집합)

관계와 관계집합

관계란 한 개체와 다른 개체가 서로 어떤 관계인지 연관성을 지칭하는 말이다.

관계 집합이란 한 개체 집합과 다른 개체 집합간의 관계를 뜻한다.

관계 집합의 속성이란 두 개체 집합의 관계에서 생성되는 속성을 뜻한다.

재귀적 관계란 한 개체 집합이 자기 자신(개체 집합)과 관계 집합을 형성하는 관계를 지칭한다.

속성

속성이란 개체 혹은 개체 집합이 가지는 특성이며, 값을 가진다.

(1) 더 작게 나눌 수 있는가? 단순 속성과 복합 속성

구분	설명
단순 속성	더 작은 요소로 나뉠 수 없는 속성
복합 속성	더 작은 요소로 나뉠 수 있는, 값이 복합된 속성

예시 -학생이름 : 홍, 길, 동을 나누면 의미를 잃으므로 -> 단순 속성
-생년월일 : 연, 월, 일로 나눠도 의미를 가지므로 -> 복합 속성

(2) 한 개체가 가질 수 있는 값으 개수는? 단일값 속성과 다중값 속성

구분	설명
단일값 속성	개체 당 하나의 값만을 가질 수 있는 속성
다중값 속성	개체 당 여러 값을 가질 수 있는 속성

예시
-생년월일 : 학생별로 하나의 생년월일을만 가질 수 있으므로 -> 단일값 속성
-전화번호 : 휴대폰 번호, 집전화번호 등 여러 전화번호를 가질 수 있으므로 -> 다중값 속성

(3) 유추를 통해 값을 도출할 수 있는가? 유도 속성과 저장 속성

구분	설명
유도 속성	유추를 통해 도출된 속성
저장 속성	다른 값으로부터 유추해낼 수 없는 속성. (저장해놓지 않으면 유추가 불가능하다 라는 뜻)

예시
-나이 : 생년월일을 토대로 추정할 수 있는 속성이므로 -> 유도 속성
-생년월일 : 다른 무언가로 추정할 수 없는 속성이므로 -> 저장 속성

제약조건

제약조건이란 데이터(엔티티, 릴레이션)가 준수해야 하는 규칙을 지칭한다. 사상수, 참가 제약조건, 키 속성 이라는 세 가지 제약조건이 있다.

(1) 사상수 (mapping cardinality)

란 하나의 관계 집합에서, 한쪽의 개체집합 X에 속한 개체(엔티티)가 다른 개체집합의 Y의 개체(엔티티) 중 몇 개의 개체와 관계를 맺을 수 있는지 그 수량을 지칭하는 용어이다.

사상수	설명
일대일 (1:1) 관계	개체집합 X의 한 개체가 상대 개체집합 Y의 개체 중 최대 한 개의 개체와만 관계를 맺을 수 있는 경우.
일대다 (1:N) 관계	개체집합 X의 한 개체가 상대 개체집합 Y의 여러 개체와 관계를 맺을 수 있으며, 개체집합 Y에 속한 개체는 개체집합 X의 개체 중 하나의 개체와만 관계를 맺을 수 있는 경우
다대일 (N:1) 관계	개체집합 X의 한 개체는 개체집합 Y의 한 개체와만 관계를 맺을 수 있으며, 개체집합 Y의 한 개체는 개체집합 X의 여러 개체와 관계를 맺을 수 있는 경우
다대다 (N:N) 관계	개체집합 X와 개체집합 Y의 개체가 상대 개체집합의 여러 개체와 관계를 맺을 수 있는 경우.

(2) 참가 제약조건

개체집합 내의 모든 개체가 관계집합에 참여하는지 여부에 따른 제약사항.

참가 제약조건	설명
전체적(total) 참가	개체 집합의 모든 개체가 관계 집합에 참여하는 제약조건
부분적(partial) 참가	개체 집합의 일부 개체가 관계 집합에 참여하는 조건

(3) 키 속성

키란 개체집합 내의 각 개체를 구별하는 데 사용되는 유일한 값을 가지는(unique) 속성 또는 속성의 집합(결합)을 지칭한다.

ER 모델의 기호

개체 집합과 속성

(1) 개체 집합

기호	관련 개념	설명
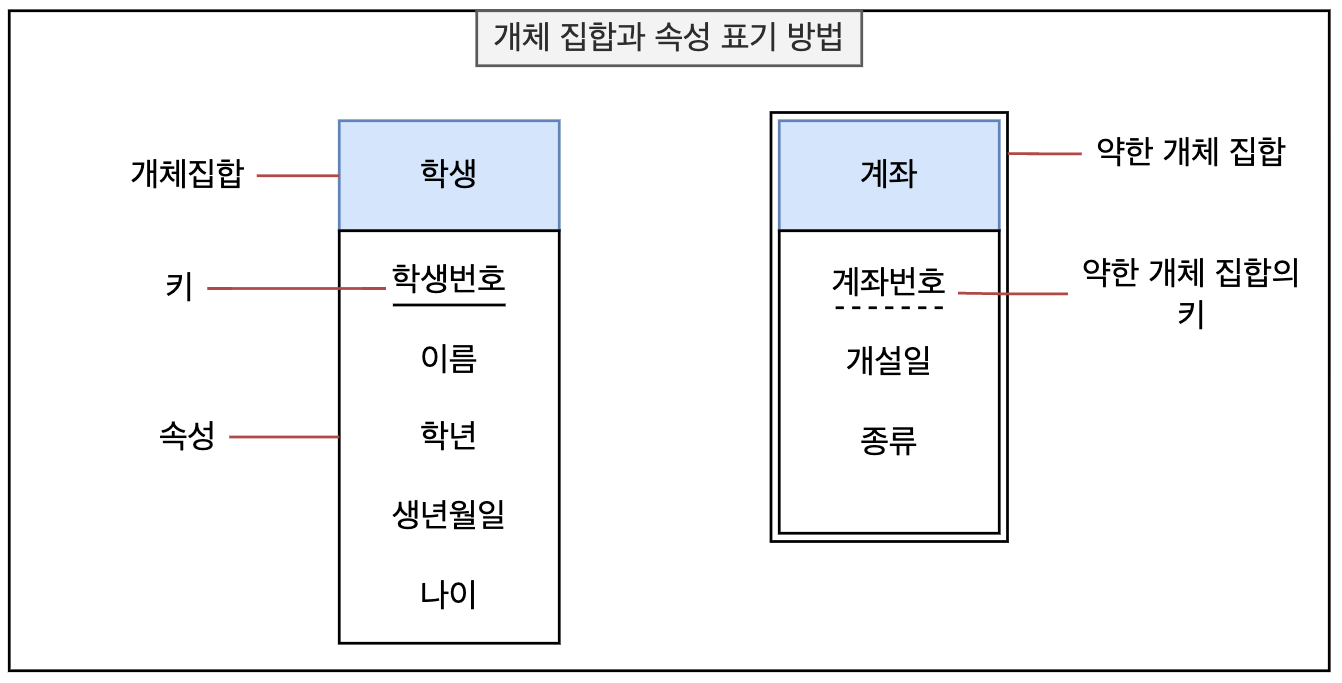
이분 직사각형	개체 집합	- 개체 집합을 표현한다. - 윗 사각형에는 개체 집합의 이름을 표기한다. - 아랫 사각형에는 개체 집합을 구성하는 속성들의 이름을 표기한다. - 기본키는 밑줄로 표시된다.
이중 이분 직사각형	약한 개체 집합	약한 개체 집합을 표현하는 방법.

(2) 속성

기호	관련 개념	설명
실선 밑줄	키	키 속성을 표시하는 벙법이다.
점선 밑줄	약한 개체 집합, 키	약한 개체 집합의 키 속성을 표시하는 방법이다.

관계 집합

기호	관련 개념	설명
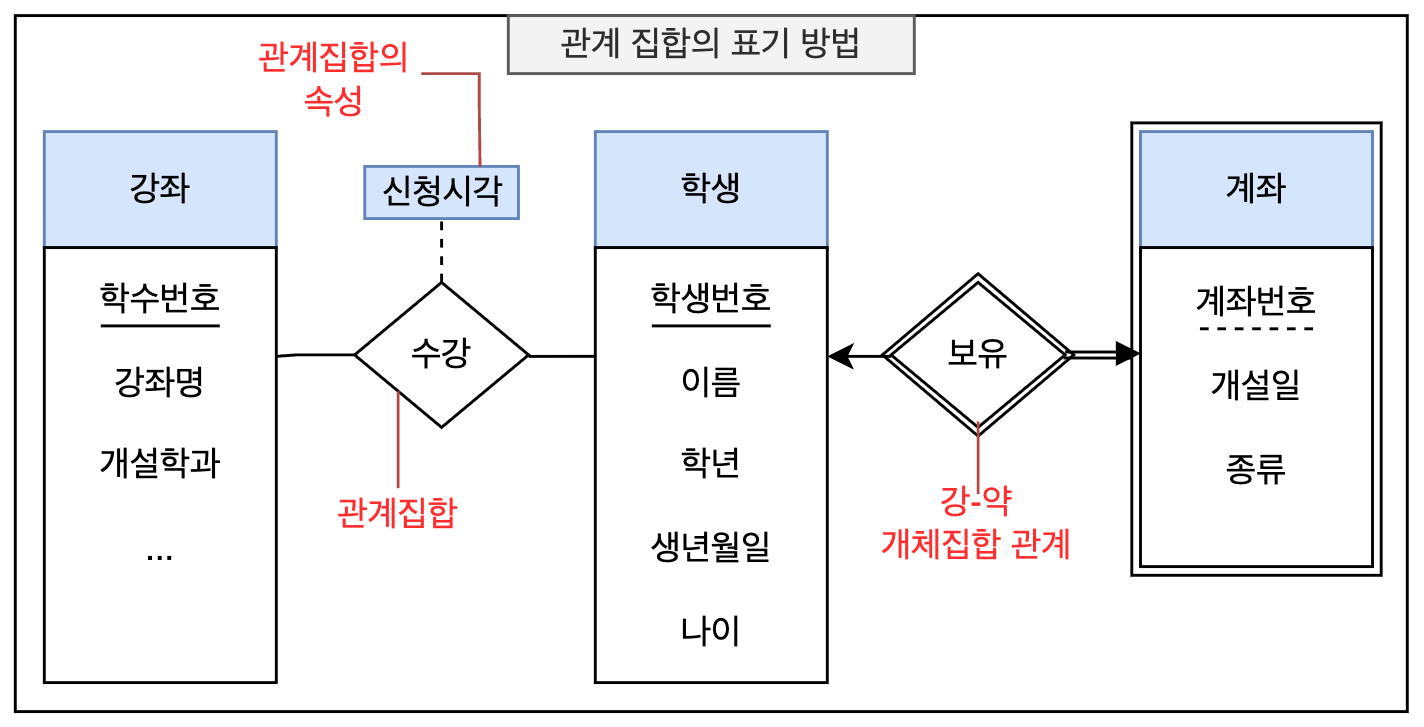
다이아몬드	관계 집합	관계 집합을 나타낸다.
이중 다이아몬드	약한 관계 집합	강한 개체 집합 - 약한 개체 집합 간의 관계(약한 관계 집합)을 나타낸다.
단일 직사각형	관계 집합의 속성	관계 집합의 속성(개체 집합 간 관계의 결과로 생성되는 값을 대표하는 속성)을 나타낸다.

개체 집합과 관계 집합의 연결

기호	관련 개념	설명
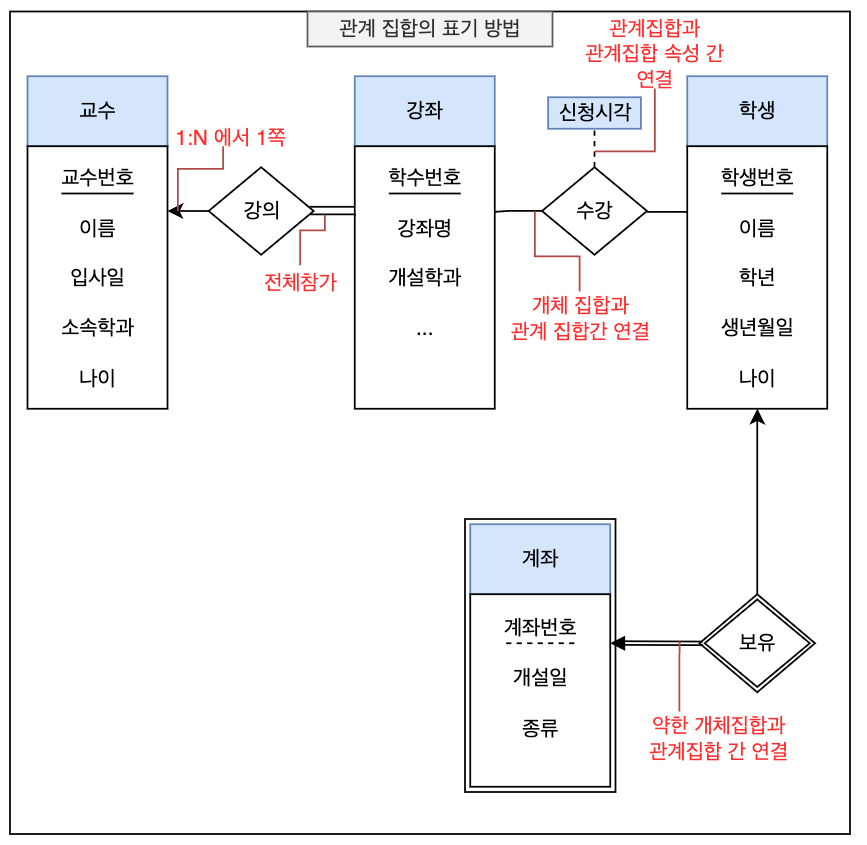
실선	-	개체 집합과 관계 집합을 연결하는 표시이다.
이중선	전체적 참가	해당 개체 집합이 해당 관계에 전체 참여하는 것을 의미한다.
이중선	약한 개체 집합	강-약 개체 집합에서 해당 개체 집합이 약한 개체 집합인 경우를 표시.
점선	관계 집합의 속성	관계 집합과 관계 집합의 속성을 연결하는 표시이다.
화살표	사상수	사상수 표현에서 ‘1’ 쪽에 화살표가 향하도록 표시한다. 양쪽 모두 1인 1:1 관계는 양쪽 개체집합에 모두 화살표가 향하도록 한다.

Reference

데이터베이스시스템 (정재화 저)