힙
힙의 개념
부모 노드와 자식 노드 사이에 일정한 대소관계를 정의해 구성한 완전 이진 트리.
주로 최댓값이나 최솟값을 빠르게 찾아내기 위해 사용되며, 우선순위 큐의 구현 등에 활용된다.
항상 가장 위에 있는 것을 우선 꺼내는 구조로, 다음섹션의 우선순위 큐를 통하여 매커니즘을 이해하면 편하다.
어떤 데에서는 힙이 우선순위 큐의 한 종류라고도 하고, 다른 곳에서는 우선순위 큐는 힙을 통해 구현된다고도 한다. 원만한 합의를 했으면 좋겠다.
부모노드는 자식노드보다 우선순위가 높다.
우선순위 큐
우선순위 큐의 개념
각 요소에 부여된 우선순위에 따라 요소를 처리하는 추상 자료형.
일반적인 큐가 FIFO 원칙을 따르는 반면, 우선순위 큐는 우선순위가 높은 요소를 먼저 처리한다.
우선순위 큐의 연산
| 연산 | 설명 |
|---|---|
| 삽입 | 요소를 우선순위와 함께 큐에 추가한다. |
| 최고 우선순위 요소 제거 | 가장 높은 우선순위를 가진 요소를 큐에서 제거하고 반환한다. |
우선순위 큐의 예시
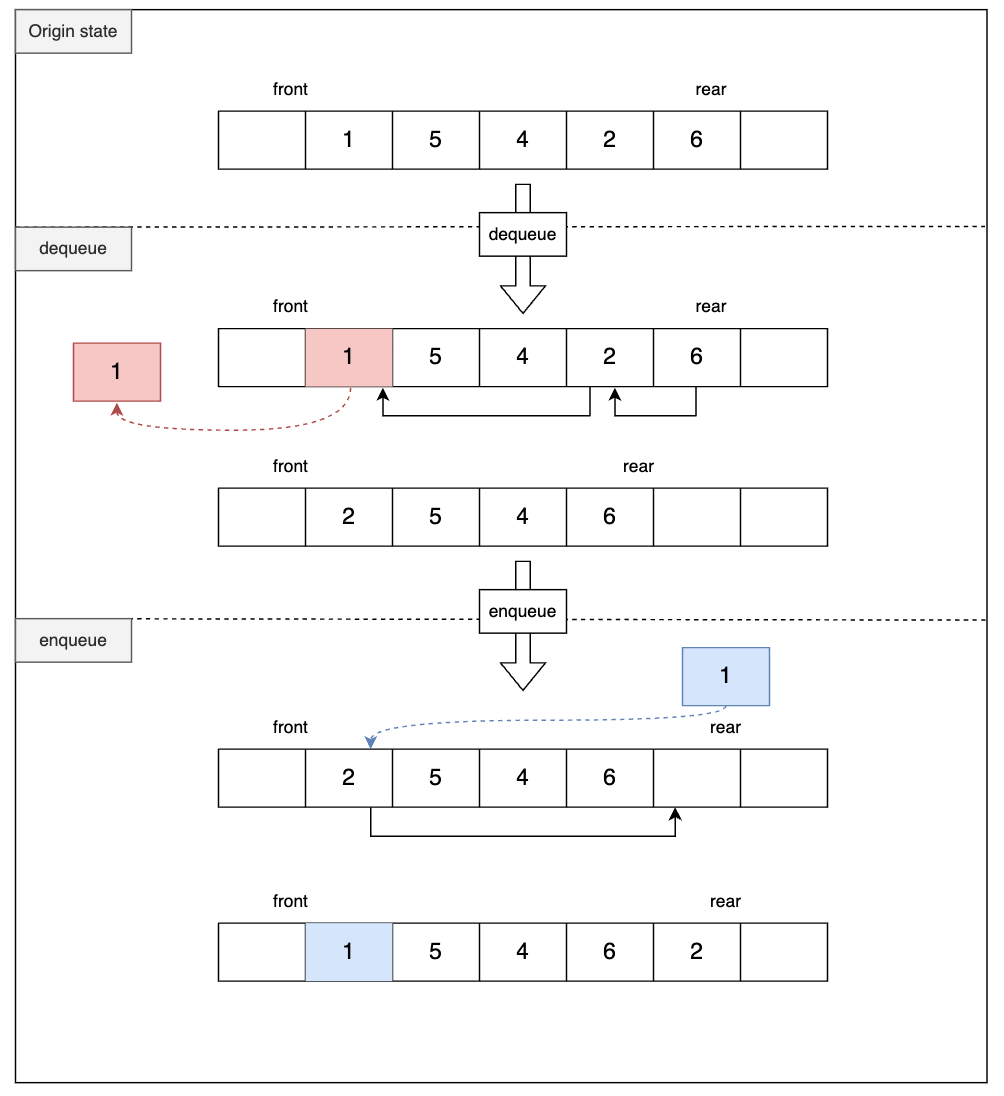
예를 들어, 값이 작은 것이 우선순위가 높은 우선순위 큐가 있다고 가정할 때,
(1) 제거(삭제) 연산이 있는 경우, front 가 가리키는 원소를 제거하고, 남은 원소들 중 가장 우선순위가 높은 원소가 front 자리로 이동한다. 빈 자리는 그 다음 원소가 메꾼다.
(2) 삽입 연산이 있는 경우, front에 있는 원소와 우선순위를 비교하여, 우선순위가 높은 원소가 front 자리를 차지하고, 나머지가 rear 자리에 삽입된다.
(3) 나머지 데이터는 어떤 순서로 저장되든 문제가 되지 않는다.
힙의 종류
| 힙의 종류 | 설명 |
|---|---|
| 최대 힙 | 루트가 가장 큰 값을 가지고 부모는 자식보다 큰 값을 가지는 완전 이진 트리 |
| 최소 힙 | 루트가 가장 작은 값을 가지고 부모는 자식보다 작은 값을 가지는 완전 이진 트리 |
힙의 추상 자료형과 연산
힙의 추상 자료형
1
2
3
4
5
6
7
8
9
10
11
ADT
1. 힙 객체의 정의
부분적으로 정렬된 완전 이진 트리로, 부모 노드는 자식 노드보다 우선순위가 높다.
2. 연산
(1) insert(element) ::= 힙에 데이터 삽입
(2) delete() ::= 힙(루트)에서 데이터 삭제
(3) peek() ::= 힙(루트)에서 데이터 읽어 오기
(4) isEmpty() ::= 힙이 비었는지 확인
(5) size() ::= 힙에 저장한 데이터 개수 확인
힙의 연산
| 연산 | 설명 |
|---|---|
| 삽입 연산 | (1) 노드 추가 : 힙의 마지막 위치에 새로운 노드를 추가 (완전 이진 트리 특성 유지 위함) (2) 힙 특성 복원 : 추가된 노드의 값이 부모와 자식 간 관계 률에 맞지 않을 경우, 부모 노드와 교환한다. (관계 률에 만족될 때까지) |
| 삭제 연산 | (1) 로트 노드 제거 : 힙의 루트 노드를 제거한다. (2) 마지막 노드 이동 : 힙의 마지막 노드를 루트 위치로 이동한다. (3) 이동된 노드와 자식 노드들을 비교해 우선순위가 더 높은 자식 노드와 자리를 교환한다. (4) 부모-자식 노드 관계가 만족될 때까지 반복한다. |

Comments