이진 트리
이진 트리의 개념
- 트리에 속한 모든 노드의 차수가 2 이하인 트리
이진 트리의 장점
- 수학적으로 이진 트리의 구성에 관한 이론 정리가 쉬움
- 컴퓨터 내부에서 구현하기도 효율적임
- 모든 노드가 2개 이하의 자식 노드를 가지므로 일반성을 가짐
- 왼쪽, 오른쪽이라는 방향 개념을 부여할 수 있음
이진 트리의 종류
| 이진 트리의 종류 | 영문 명칭 | 설명 |
|---|---|---|
| 가득 찬 이진 트리 | perfect binary tree | 모든 내부 노드가 두 개의 자식을 가지고 있으며 모든 리프 노드가 동일한 깊이에 있는 이진 트리 |
| 완전 이진 트리 | complete binary tree | 모든 레벨이 완전히 채워져 있으며 마지막 레벨의 노드들이 왼쪽에서부터 연속적으로 배치된 이진 트리 |
| 전 이진 트리 | full binary tree | 모든 노드가 0개 또는 2개의 자식을 가지는 이진 트리 |
이진 트리의 구현
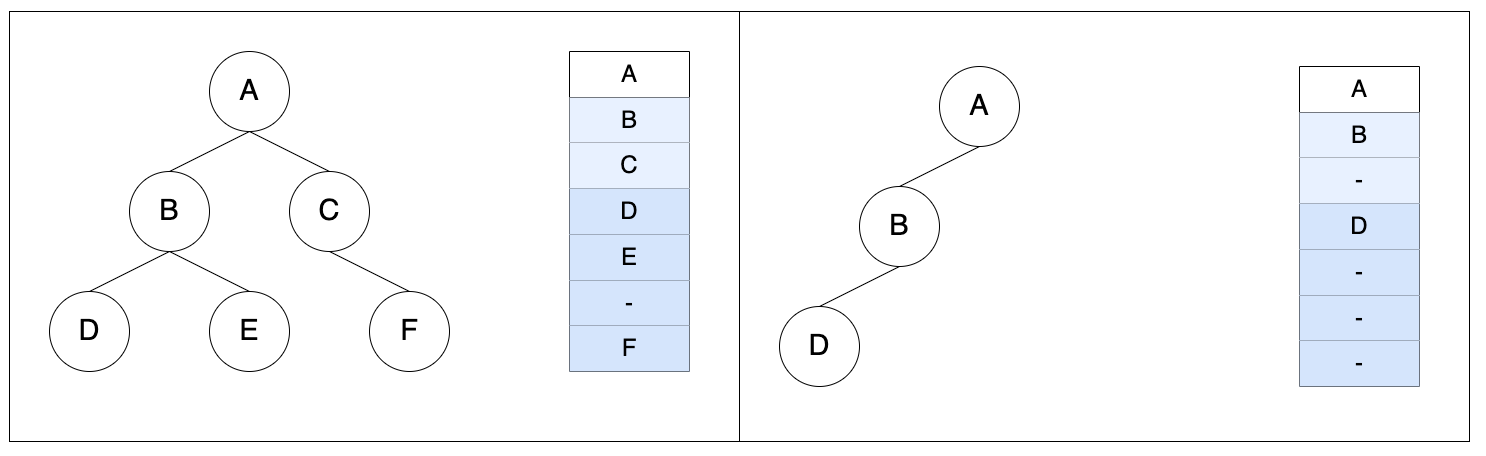
배열을 이용한 이진 트리의 구현
- 완전 이진 트리 혹은 가득 찬 이진 트리인 경우 낭비 공간이 없어 효율적임
- 그게 아닌 경우, 트리가 깊어질수록 기억장소 낭비가 2의 거듭제곱에 비례하게 심해짐
때문에 이진 트리는 보통 연결리스트로 구현됨
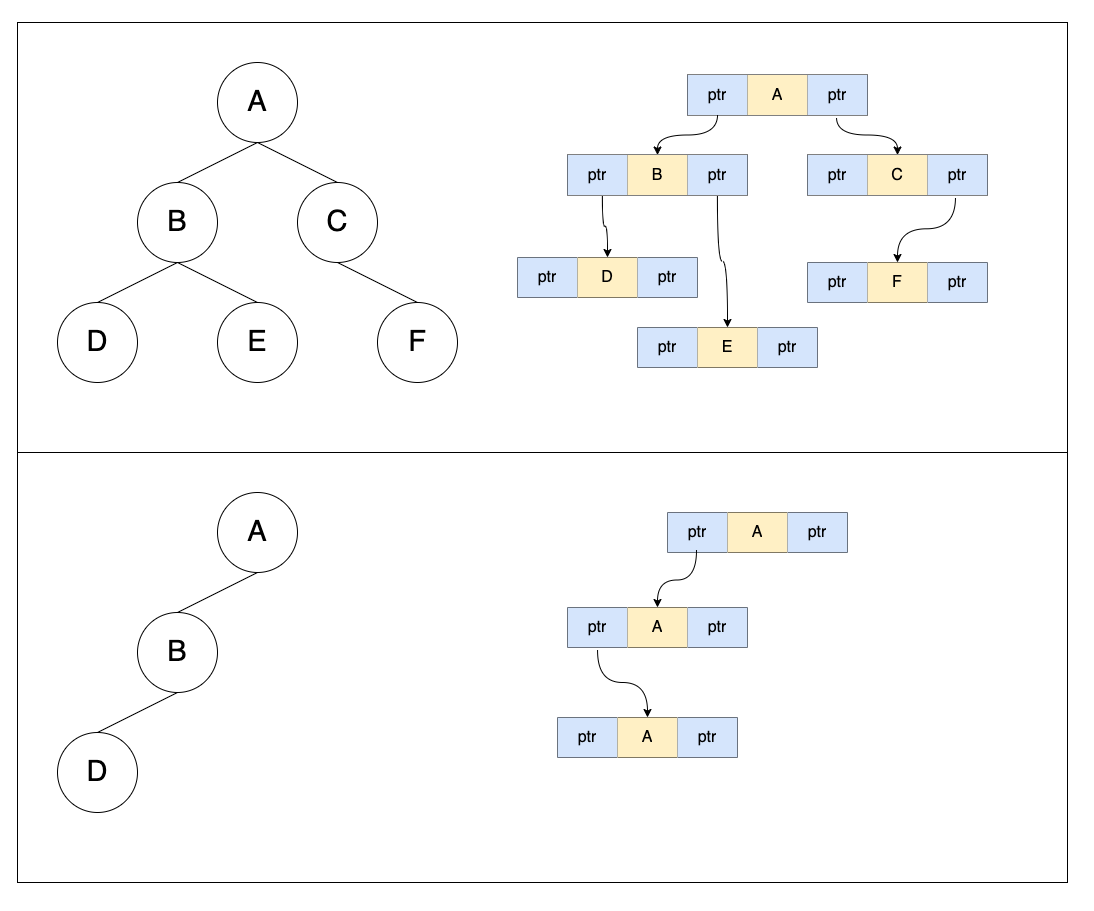
포인터(연결 리스트)를 이용한 이진 트리의 구현
- 이진 트리를 연결 리스트로 구축하는 방법
- 데이터, 왼쪽 서브트리 포인터, 오른쪽 서브트리 포인터로 구성됨
- 노드의 차수가 크면 그만큼 많은 포인터를 유지해야 하는 단점
이진 트리의 연산
이진 트리의 순회
- 이진트리의 순회 : 이진 트리의 각 노드를 빠짐없이, 그리고 중복없이 한 번씩 꼭 방문하는 것
| 구분 | 설명 |
|---|---|
| 이진트리의 전위 순회 | 루트로부터 -> 왼쪽 서브트리 -> 오른쪽 서브트리 순으로 순회하는 방법 |
| 이진트리의 중위 순회 | 인쪽 서브트리로부터 -> 루트 -> 오른쪽 서브트리 순으로 순회하는 방법 |
| 이진트리의 후위 순회 | 왼쪽 서브트리로부터 -> 오른쪽 서브트리 -> 루트 순으로 순회하는 방법 |
주의할 점은 “모든 서브트리마다” 순회 방법을 따른다는 점이다. 이게 무슨 말인지 그림으로 좀 더 명확하게 이해해보자.
이진트리의 전위 순회
루트로부터 -> 왼쪽 서브트리 -> 오른쪽 서브트리 순으로 순회하는 방법
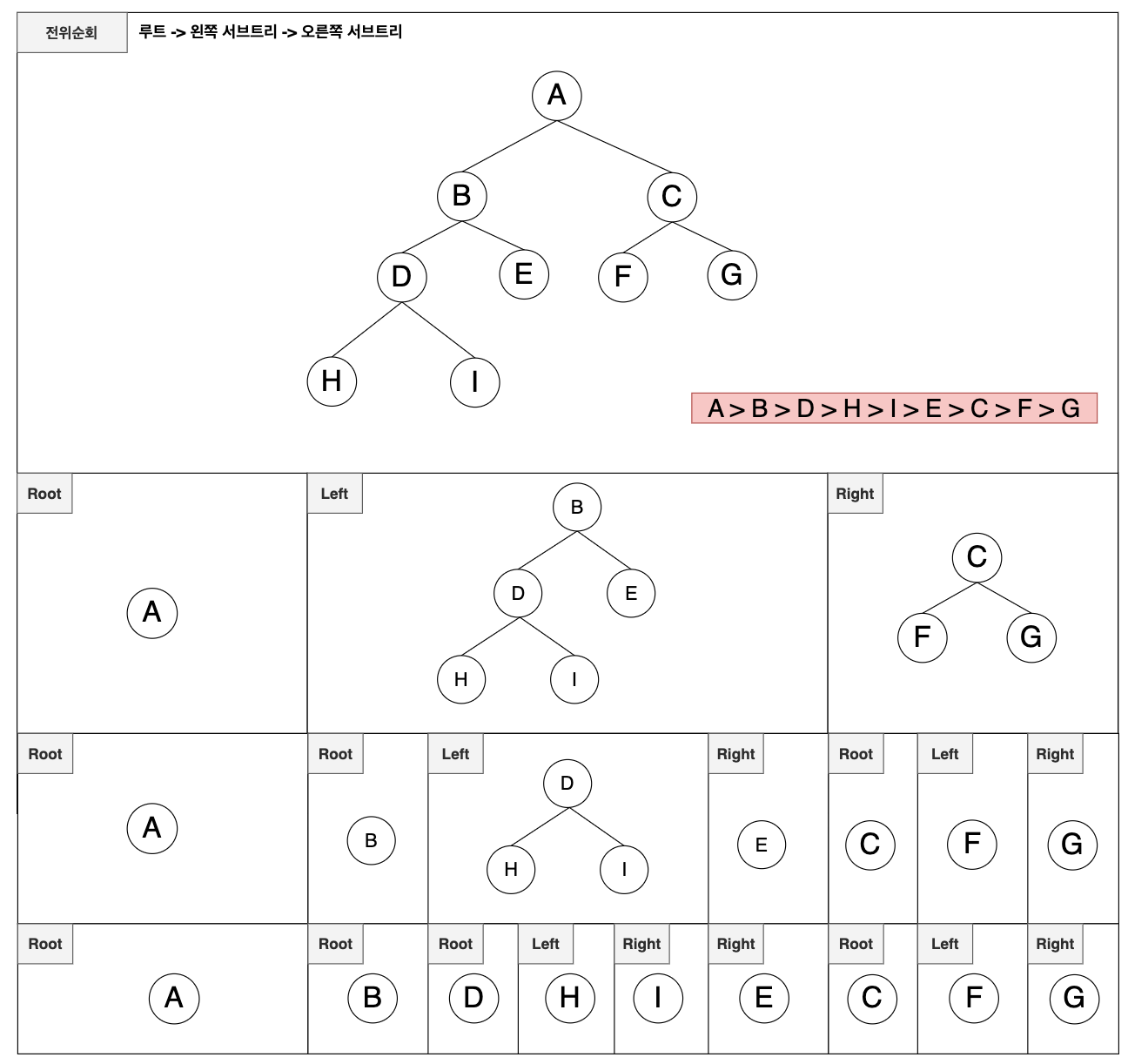
이진트릐의 중위 순회
인쪽 서브트리로부터 -> 루트 -> 오른쪽 서브트리 순으로 순회하는 방법
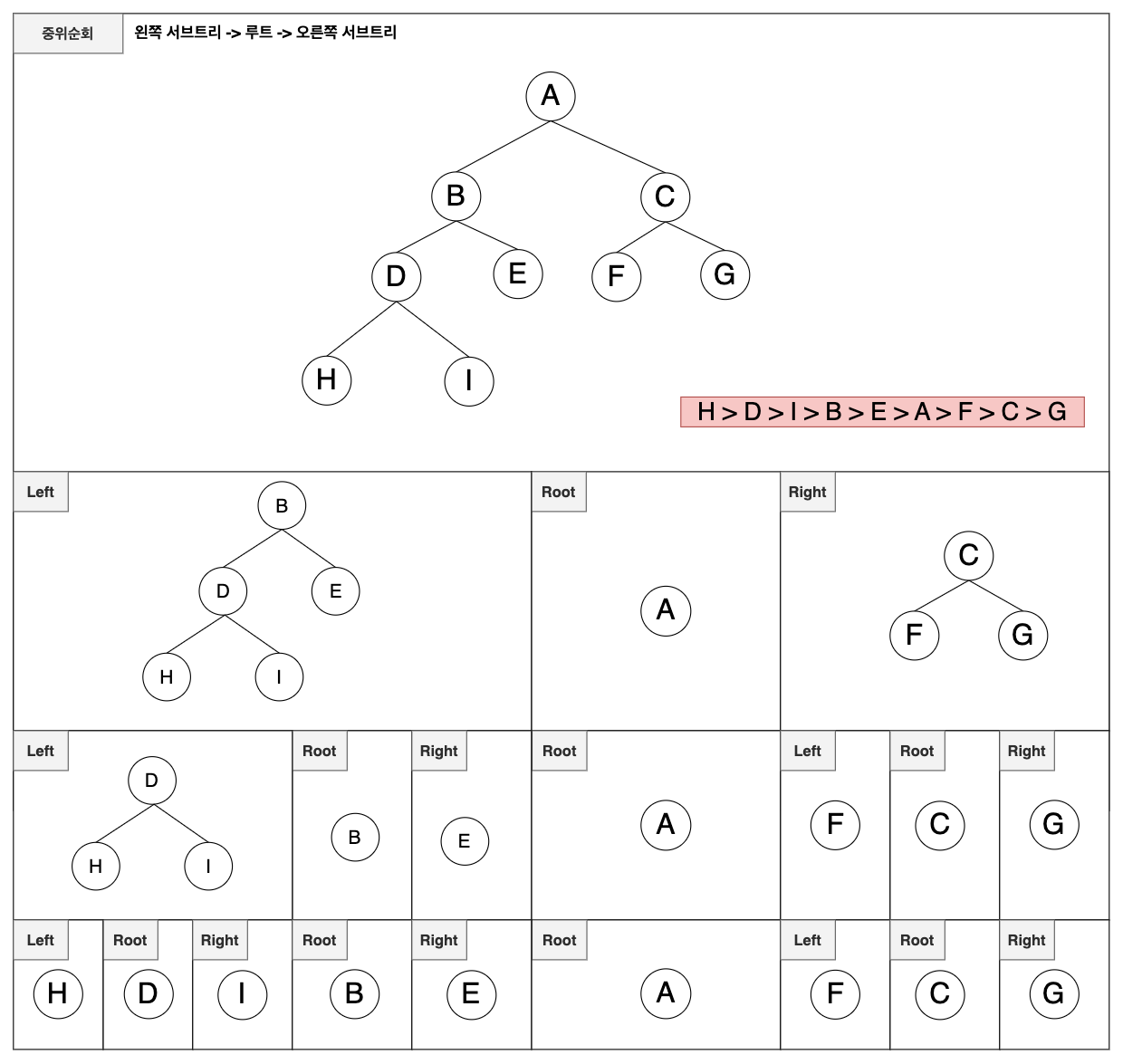
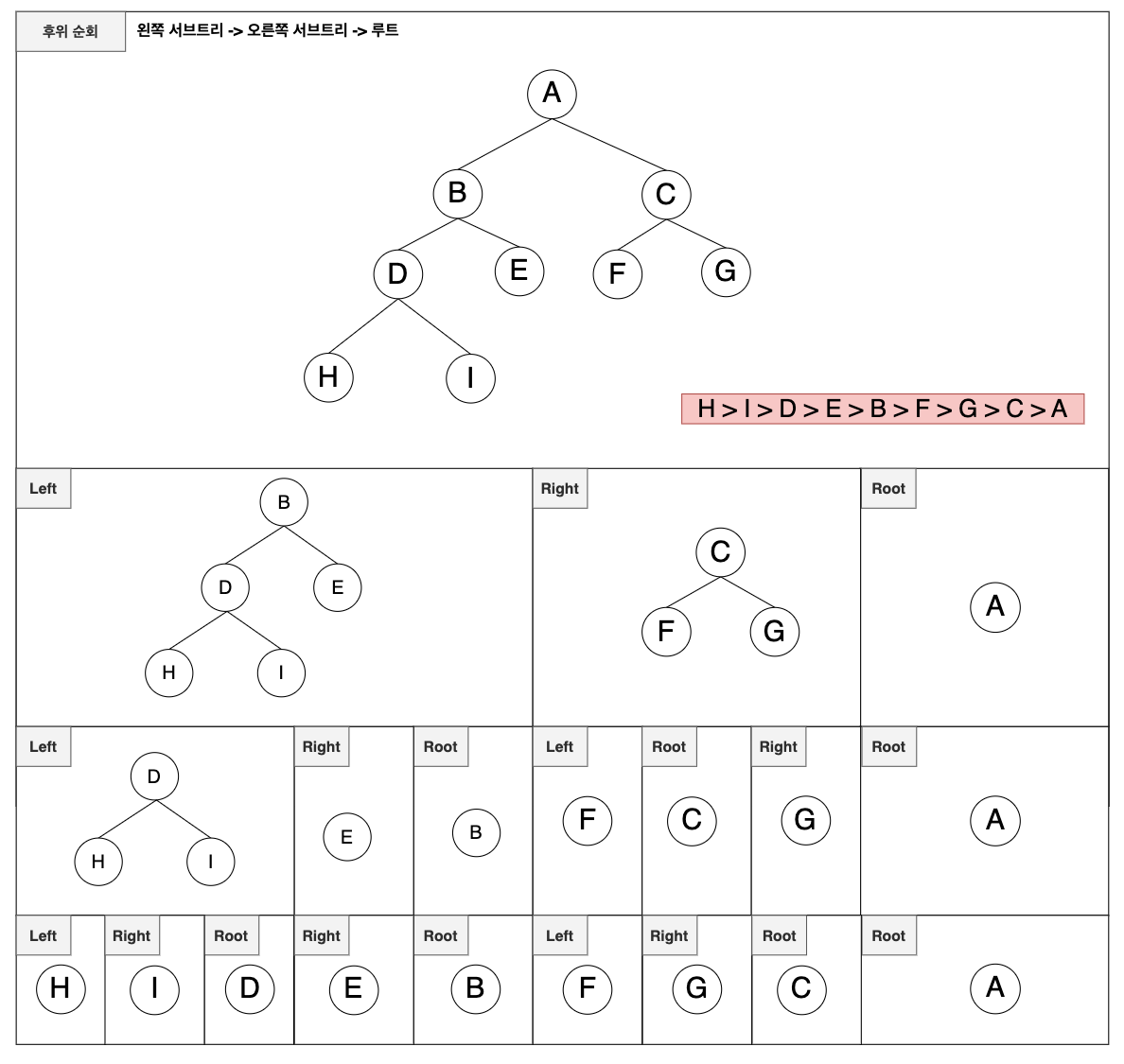
이진트리의 후위 순회
왼쪽 서브트리로부터 -> 오른쪽 서브트리 -> 루트 순으로 순회하는 방법
이진 트리의 생성
앞선 단락인 이진 트리의 구현 - 연결 리스트 이용한 부분 참고
이진 트리의 삽입
- 이진 트리를 일반적으로 연결 리스트로 구축한다는 전제 하에
- 이진 트리의 노드 생성은 부모 노드의 포인터 중 하나가 새로 추가하는 노드를 가리키도록 설정하면 된다.
- 만약 기존 존재하던 노드를 새로운 노드로 대체할 경우, 원래 노드를 어떻게 처리할 것인지 방치하지 않고 결정하는 게 권장된다.
이진 트리의 삭제
- 이진 트리를 일반적으로 연결 리스트로 구축한다는 전제 하에
- 이진 트리의 노드 삭제는 부모 노드에서 삭제하려는 노드를 가리키던 포인터가 가리키는 주소를 NULL로 만든다.
- 자식 노드였던 것을 삭제하는 등의 처리를 진행한다.
이진 트리 노드 개수 세기
(1) 이진 트리의 노드 개수 세기
1
2
3
4
5
6
7
8
9
10
int get_nodeNum(node *root) {
int num = 0;
if (root == NULL) {
return 0;
} else {
num = 1;
num += (get_nodeNum(root -> left) + get_nodeNum(root -> right));
return num;
}
}
(2) 이진 트리의 잎 노드 개수 세기
1
2
3
4
5
6
7
8
9
10
11
int get_leafNum(node *root) {
int result = 0;
if (root == NULL) {
return 0;
} else if (root -> left == NULL && root -> right == NULL) {
return 1;
}
result += get_leafNum(root -> left) + get_leafNum(root -> right);
return result;
}
일반 트리의 이진 트리로 변환
(1) 각 노드의 형제들을 연결한다.
(2) 각 노드에 대해 가장 왼쪽 링크만 남기고 모두 제거한다.
(3) 루트 노드는 반드시 왼쪽 자식 하나만 가지도록 한다.

Comments