자료구조 - 트리

트리

트리의 개념

• 논리적 계층이 있는, 계층적 관계를 표현하는 비선형 자료구조.
• 노드(Node)와 간선(Edge)로 구성되어있다.
• 각 노드는 부모 - 자식 관계를 통해 연결된다.
• 루트 노드로부터 시작하여 여러 자식 노드를 가질 수 있다.

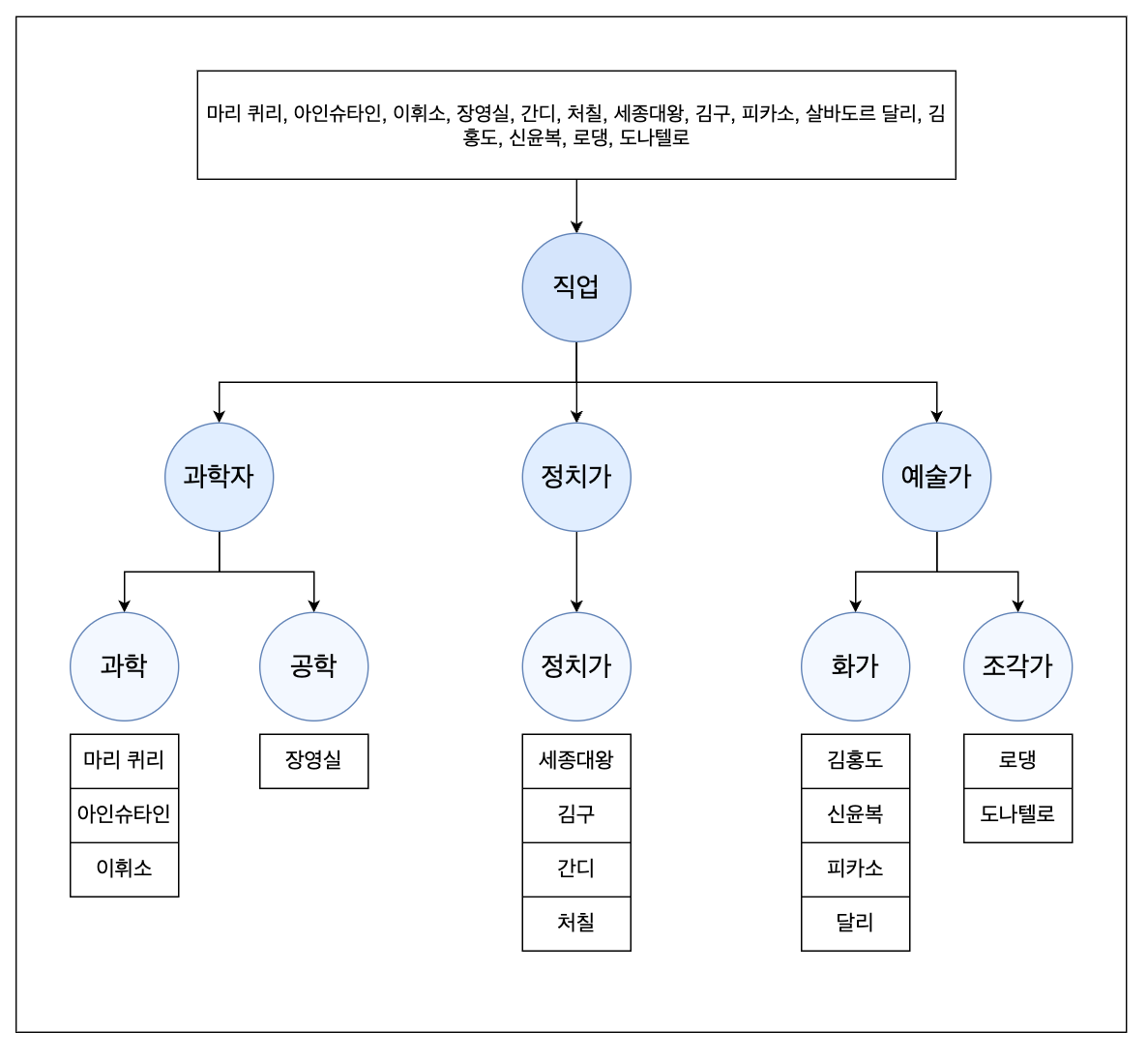
트리 자료구조의 장점

(1) 구조화된 자료를 한눈에 볼 수 있음
(2) 효율적인 탐색 및 삽입
(3) 명확한 계층적 데이터 표현
(4) 유연한 데이터 구조
(5) 효율적 데이터 정렬
(6) 메모리 효율성
등..

트리의 구성 요소와 표현 방법

트리의 구성 요소

구성 요소	영문명칭	설명
노드	node	트리의 기본 구성 요소로, 데이터를 저장하거나 나른 노드와 연결하는 단위
부모노드	parent node	특정 노드와 직접 연결된 바로 상위 노드
자식노드	child node	특정 노드와 직접 연결된 바로 하위 노드
루트노드	root node	트리의 최상위 노드(부모가 없는 노드)
간선	edge	노드 간의 관계를 나타내는 연결선. 한 간선은 두 노드를 연결한다.
차수	degree	하나의 노드가 가진 자식 노드의 개수
서브트리	subtree	특정 노드로부터 시작되는(=특정 노드를 루트로 하는) 트리의 일부 구조
잎 노드		트리의 맨 끝에 있으면서, 자신의 서브트리를 갖지 않는 노드
진입 차수	in-degree	특정 노드로 들어오는 간선의 수
진출 차수	out-degree	특정 노드에서 나가는 간선의 수
내부 노드	internal node	루트 노드와 잎 노드를 제외한 나머지 노드
형제	sibling	같은 부모 노드를 공유하는 노드
경로	path	한 노드가 다른 노드로 가는 노드 간의 연결 관계
경로의 길이	path length	경로를 따라 이동할 때 지나가는 간선의 개수
레벨	leve	트리 내의 특정 노드가 루트 노드에서부터 떨어진 거리(깊이)

트리의 표현 방법

패스

트리의 추상 자료형

ADT

1. 트리 객체에 대한 정의
- 루트 노드를 갖는 유한 리스트  

2. 트리의 연산  
(1) Tree Create() ::= 트리를 생성하고, 루트 노드를 가리키는 포인터를 반환한다.
(2) Destroy(Tree) ::= 사용하지 않는 트리의 기억 장소를 시스템에 반환한다.
(3) Tree Copy_Tree(Tree) ::= 트리를 복사하고, 새로 생성한 트리의 루트 노드를 가리키는 포인터를 반환한다.
(4) Insert(n) ::= 트리에 노드 n을 삽입한다.
(5) Delete() ::= 트리에서 노드를 삭제한다. 보통 재구성 단계를 포함한다.
(6) Search() ::= 트리에서 특정 키값을 갖는 노드를 찾는다. 찾았다면 true, 못찾았다면 false를 반환한다.
(7) Traverse() ::= 트리를 순회하고, 방문 순서대로 값을 반환한다.
(8) Root() ::= 루트 노드 값을 반환한다.
(9) Parent(n) ::= 노드 n의 부모(값이나 포인터)를 반환한다. n이 루트이면 오류를 반환.
(10) Children() ::= 노드 n의 자식(값 혹은 포인터)를 반환한다. n이 잎이면 오류를 반환한다.
(11) IsRoot(n) ::= 노드 n이 루트이면 true, 아니면 false를 반환한다.
(12) IsInternal(n) ::= 노드 n이 내부 노드이면 true, 아니면 false를 반환한다.
(13) IsLeaf(n) ::= 노드 n이 잎이면 true, 아니면 false를 반환한다.
(14) IsEmpth() ::= 트리가 비었다면 true, 아니면 false를 반환한다.
(15) Replace(n,m) ::= 노드 n을 노드 m으로 바꾼다.

트리 자료구조의 종류

트리 자료구조
├── 일반 트리 (General Tree)
├── 이진 트리 (Binary Tree)
│   ├── 포화 이진 트리 (Full Binary Tree)
│   ├── 완전 이진 트리 (Complete Binary Tree)
│   ├── 편향 이진 트리 (Skewed Binary Tree)
│   ├── 이진 검색 트리 (Binary Search Tree, BST)
│   ├── 균형 트리 (Balanced Tree)
│   │   ├── AVL 트리 (AVL Tree)
│   │   └── 레드-블랙 트리 (Red-Black Tree)
│   └── **스레드 트리 (Threaded Tree)**  <-- 여기에 위치
├── 힙 (Heap)
│   ├── 최대 힙 (Max Heap)
│   └── 최소 힙 (Min Heap)
├── N-진 트리 (N-ary Tree)
├── 트라이 (Trie, Prefix Tree)
├── 세그먼트 트리 (Segment Tree)
├── 스패닝 트리 (Spanning Tree)
├── B-트리와 B+트리
│   ├── B-트리 (B-Tree)
│   └── B+트리 (B+Tree)
├── 이진 인덱스 트리 (Fenwick Tree)
├── 결정 트리 (Decision Tree)
└── 컴프레션 트리
    ├── 서픽스 트리 (Suffix Tree)
    └── 라딕스 트리 (Radix Tree)

Reference

자료구조 (강태원, 정광식 공저)