스택
스택의 개념
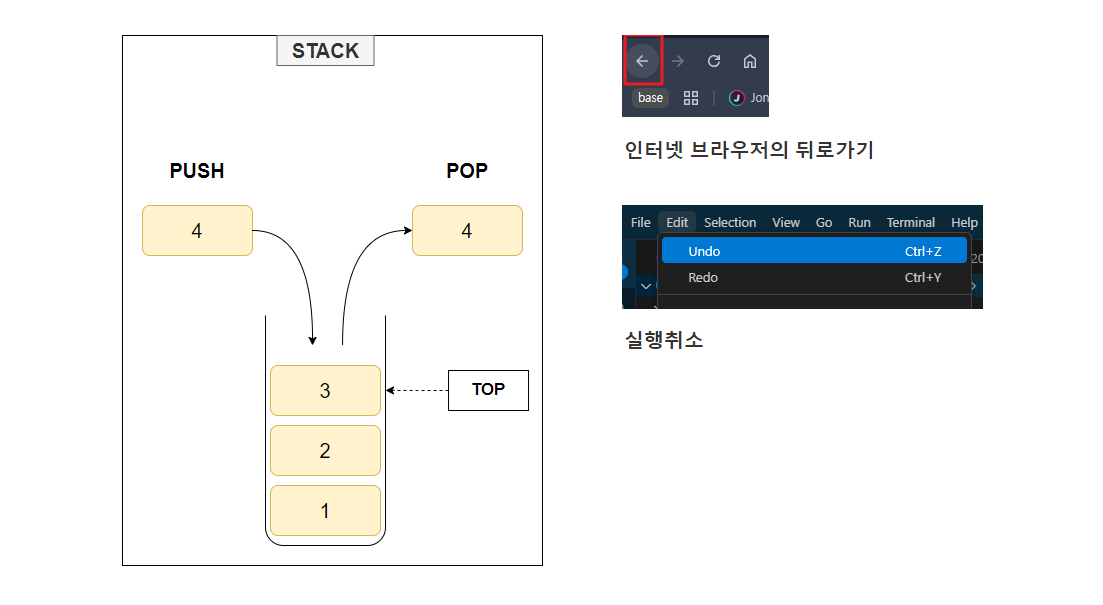
- 한 쪽 끝이 막혀있는 관과 같은 형태. 그 관은 물체를 한 쪽 끝으로만 넣을 수 있고, 동일한 끝에서만 뺄 수 있다.
- 0개 이상의 원소를 가지며, 원소가 저장되고 삭제되는 특정 순서를 가진 유한 순서 리트스.
- 스택은 리스트에 원소를 삽입하는 푸시와 원소를 삭제하는 팝이라는 연산을 가진다.
- 가장 먼저 삽입된 원소가 가장 나중에 삭제되는 후입 선출 (LIFO, Last-In-First-Out) 원칙을 따른다.
- 원소의 삽입과 삭제가 스택의 한 쪽 끝에서만 일어나며, 이곳을 탑 (TOP) 이라고 한다.
- Top의 위치는 -1 부터 시작된다.
- 스택은 크기 제한이 있다. (무한하지 않다.)
스택의 추상 자료형과 연산의 구현
스택의 추상 자료형
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
ADT
1. 스택 객체에 대한 정의
- 스택 객체 : 0개 이상의 원소를 갖는 유한 순서 리스트
- 연산의 위치 : push(add) 와 pop(delete) 연산이 한 곳(top) 에서 발생되는 자료구조
2. 스택의 연산
- stack : 0개 이상의 원소를 갖는 스택
- item : 스택에 삽입되는 원소
- maxStackSize : 스택의 최대 크기
- stack ∈ Stack, item ∈ Element, maxStackSize ∈ positive integer 라고 할 때
(1) Stack CreateStack(maxStackSize) ::=
스택의 크기가 maxStackSize인 빈 스택을 생성하고 반환한다.
(2) Boolean StackIsFull(stack, maxStackSize) ::=
if((stack의 elements의 개수) == maxStackSize)
then return True
else return False
(3) Stack Push(stack, item) ::=
if(StackIsFull(stack))
then { 'stackFull' 을 출력한다; }
else { 스택의 가장 위(뒤)에 item을 삽입하고 스택을 반환한다; }
(4) Boolean StackIsEmpty(stack) ::=
if(stack == CreateStack(maxStackSize))
then return True
else return False
(5) Element Pop(stack) ::=
if(StackIsEmpty(stack))
then { 'stackEmpty' 를 출력한다; }
else { 스택의 가장 위에 있는 원소(element)를 삭제하고 반환한다; }
스택 연산의 구현
(5) 스택의 삭제 연산
1
2
3
4
int pop() {
if (top == -1) // top 값이 -1 (빈 상태) 면
return StackEmpty(); // stackEmpty 메시지 출력하는 함수
else return stack[top--]; } // stack[top] 값을 반환하고, top 에서 1을 감소시킴
(3) 스택의 삽입 연산
1
2
3
4
5
void push(int item) {
if (top >= STACK_SIZE -1) // top 이 스택사이즈-1(max 인덱스) 보다 크거나 같다면
return StackIsFull(); // 스택이 가득 찼다는 메시지 출력하는 함수
else stack[++top] = item; // top 값을 하나 증가시키고, stack 의 top 인덱스에 해당하는 주소에 item 을 저장
}
스택의 응용
- 시스템 스택 : 변수에 대한 메모리 할당과 수집 (변수의 생명주기 관리)
- 서브루틴 호출 관리 : 서브루틴의 수행이 끝난 후에 되돌아갈 함수 주소를 저장하기 위함
- 후위 수식 계산 : 컴퓨터가 사칙연산의 계산 순위를 결정하는 데 이용
- 인터럽트 처리, 인터럽트 후 되돌아갈 명령 수행 지점 저장
- 컴파일러
- 순환호출
- 등, 입력값의 입력 순서나 사건의 선후 순서를 기억하기 위해 사용되는 자료구조
스택을 이용한 후위 표기식의 계산
스택을 이용한 중위 표기식을 후위 표기식으로 변환하기
(1) 중위 표현식의 앞(왼쪽) 부터 읽어들인다.
(2) 읽어들인 게 피연산자라면 그대로 변환필드로 출력한다.
(3) 읽어들인 게 연산자라면 스택에 담아둔다.
(4) 스택에 이미 연산자가 담겨있을 경우(=기존 연산자), 기존 연산자와 신규 연산자의 우선순위를 비교한다.
(5) 신규 연산자의 우선순위가 높다면 그대로 기존 연산자 위쪽(나중 삽입) 스택에 쌓인다.
(6) 신규 연산자의 우선순위가 기존 연산자와 같거나 낮다면 기존 연산자는 pop 되어 변환필드로 출력되며, 신규 연산자는 스택에 쌓인다.
(7) 기존 연산자가 두 개 이상인 경우, 신규 연산자는 자신의 우선순위가 높다는 판단이 나올 때까지 모든 기존 연산자와 우선순위 비교를 한다.
(8) 1-7 단계를 반복한다.

후위 표기식 계산 알고리즘과 스택을 이용한 연산
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
element evalPostfix(char *exp) {
int oper1, oper2, value, i=0;
int length = strlen(exp);
char symbol;
top = -1;
for (i = 0; i < length; i++){
symbol = exp[i];
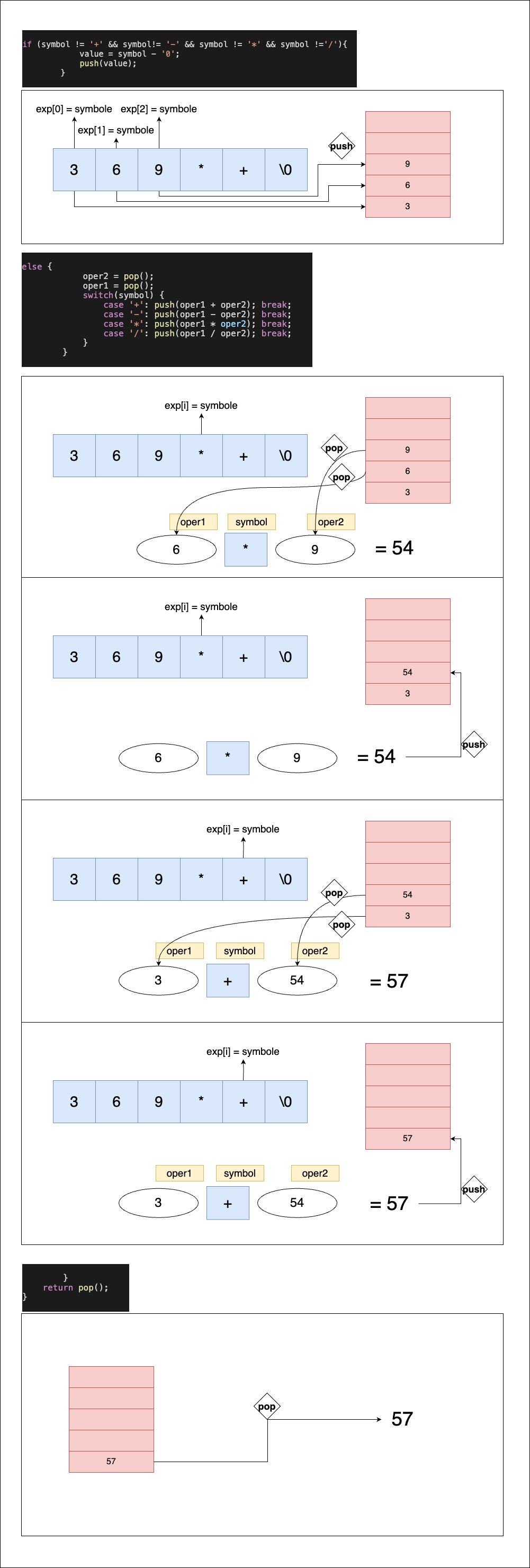
if (symbol != '+' && symbol!= '-' && symbol != '*' && symbol !='/'){
value = symbol - '0';
push(value);
}
else {
oper2 = pop();
oper1 = pop();
switch(symbol) {
case '+': push(oper1 + oper2); break;
case '-': push(oper1 - oper2); break;
case '*': push(oper1 * oper2); break;
case '/': push(oper1 / oper2); break;
}
}
}
return pop();
}

Comments