배열
배열의 개념
- 배열은 인덱스와 원소값의 쌍(
<index, value>)으로 구성된 집합이다. - 배열의 원소(인덱스와 원소값으 쌍)는 모두 같은 자료형이다.
- 배열의 원소는 모두 같은 크기의 기억 공간(메모리 크기) 를 갖는다.
- 배열의 원소들은 인덱스로 표현되는 순서를 가진다.
- 배열의 원소 간 논리적인 순서가 각 원소의 물리적인 위치(메모리 주소)의 순서와 일치한다.
배열의 인덱스값과 메모리 주소의 관계
요약
- 배열의 인덱스는 실제 메모리 주소값을 추상화한 값이다.
- 배열 내의 원소간 순서는 각 원소가 저장된 메모리 주소값 간의 순서와 동일하다.
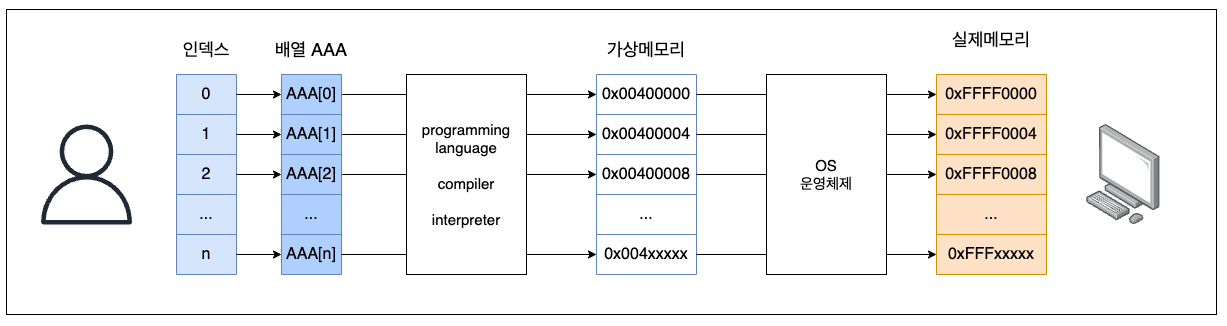
배열의 인덱스는 배열 내 값(value)의 위치를 나타내는 숫자이다. 다만 인덱스는 실제 물리적인 위치값(주소값)을 나타내는 것은 아닌 배열 내 요소의 상대적인 순서를 나타내는 논리적인 위치값이다. 이러한 상대적인 순서는 배열의 각 요소가 저장된 메모리의 주소값 간에도 동일한 순서로 적용된다.
배열의 인덱스는 0부터 시작해 순차적으로 1씩 증가하는 10진수 형태이며, 실제 메모리의 주소값은 16진수의 형태를 가지고 있다. 때문에 둘은 직접적으로 매칭이 될 수는 없으며, 이 둘 사이에서 프로그래밍 언어와 운영체제가 각각 배열의 순서와 실제 메모리의 주소값을 번역하고 매칭시켜 관리한다.
운영체제는 프로세스가 사용할 수 있는 메모리 영역을 관리하고 할당하는데, 가상 메모리를 실제 물리적 메모리에 매핑하는 역할을 담당한다. 프로그래밍 언어와 컴파일러(혹은 인터프리터)는 배열의 기초 주소(base address), 요소의 크기(size), 인덱스를 기반으로 가상 메모리의 주소를 계산한다. 이 두 가지가 결합되어 배열의 인덱스를 사용한 논리적인 위치 접근과 실제 메모리의 물리적 위치 간의 연결을 제공한다.
결론적으로 배열의 인덱스는 실제 메모리 주소값을 추상화한 값이며, 배열 내의 원소간 순서는, 배열의 각 원소가 저장된 메모리 주소값 간의 순서와 동일하다는 특징을 가지고 있다.
배열의 추상 자료형과 배열 연산의 구현
배열의 추상 자료형
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
ADT Array
1. 정의
- <i ∈ Index, e ∈ Element> 쌍들의 집합
- Index : 순서를 나타내는 원소의 유한집합
- Element : 자료형이 동일한 원소의 집합
2. 연산
- a : 0개 이상의 원소를 갖는 배열
- e : 배열에 저장되는 원소
- n : 배열의 최대 크기를 정의하는 정수값
- a ∈ Array; i ∈ Index; e ∈ Element, n ∈ Integer 라고 할 때
- a, item, n에 대해 다음과 같은 연산이 정의된다.
(1) Array create(n) ::= 배열의 크기가 n인 배열을 생성하고, 공백 배열을 반환한다. // 생성 연산
(2) Element retrieve(a, i) ::= if(i ∈ Index) // 검색 연산
then { 배열의 i 번째에 해당하는 원소값 e를 반환한다; }
else { 에러 메시지를 반환한다; }
(3) Array store(a, i, e) ::= if(i ∈ Index) // 저장 연산
then { 배열 a의 i 번째 위치에 원소값 e를 저장하고 배열 a를 반환한다;}
else { 인덱스 i가 배열 a의 크기를 벗어나면 에러 메시지를 반환한다;}
End Array
배열 연산의 구현
(1)배열의 생성
1
2
3
4
5
6
7
void create(int n) {
int a[n];
int i;
for(i=0, i<n, i++){
a[i] = 0;
}
}
(2)배열값의 검색(retrieve)
1
2
3
4
5
6
int retrieve(int *a, int i) {
if (i >=0 && i < array_size)
return a[i];
else {printf("Error₩n");
return (-1); }
}
(3)배열값의 저장(store)
1
2
3
4
5
void store(int *a, int i, int e) {
if (i >= 0 && i < array_size)
a[i] = e;
else printf("Error₩n");
}
1차원 배열
(1) 1차원 배열의 정의
1차원 배열이란, 한 줄짜리 배열을 의미한다. 따라서 하나의 인덱스로 구분된다.
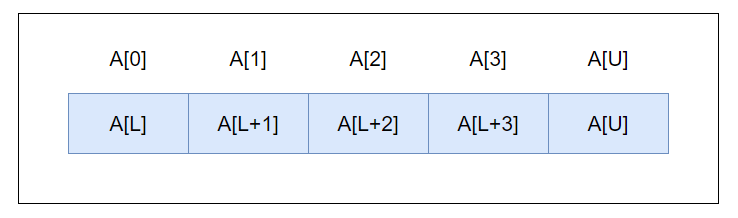
L : Lower Bound. 배열의 시작 인덱스.
U : Upper Bound. 배열의 끝 인덱스.
(2) 1차원 배열에서의 주소 계산
-배열의 원소들은 모두 동일한 크기의 자료형으로 구성되어있다.
-배열의 원소간 순서는 실제 메모리에 적재되는 공간 주소값의 순서와 동일하다.
-따라서 배열의 첫 시작 주소와 자료형의 크기를 알 수 있다면, 특정 원소의 주소값을 알 수 있다.
배열 첫 원소의 시작 주소가 H, 배열 각 원소 자료형의 크기가 k 일 때, 배열의 i 번째에 있는 원소의 메모리 주소는 H + (i * k) 이다.
배열의 확장
(1) 2차원 배열(행렬)의 표현
이번 단락에서는 행렬을 확장해보겠다. 앞서 1차원 배열을 봤다면, 그 다음은 2차원 배열이다. 2차원 배열은 배열을 원소로 가지는 배열이라고 생각하면 편하겠다.
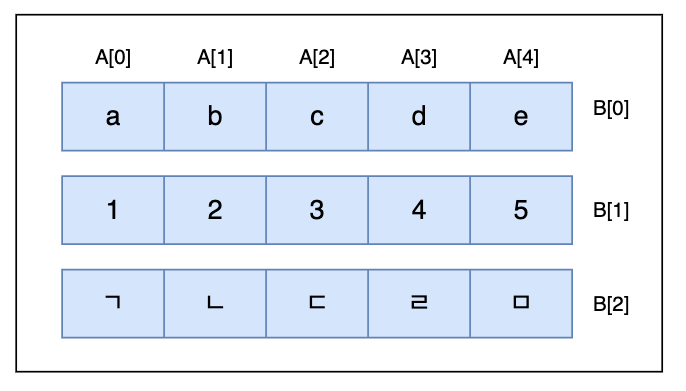
위 그림은 2차원 배열을 표현한 것이다. 파란색의 세 개의 배열이 있고, 이것이 배열 B의 각 원소로 다시 한 번 포함되는 모양이다. 이를 좀 더 자세히 나타내면 아래와 같다.
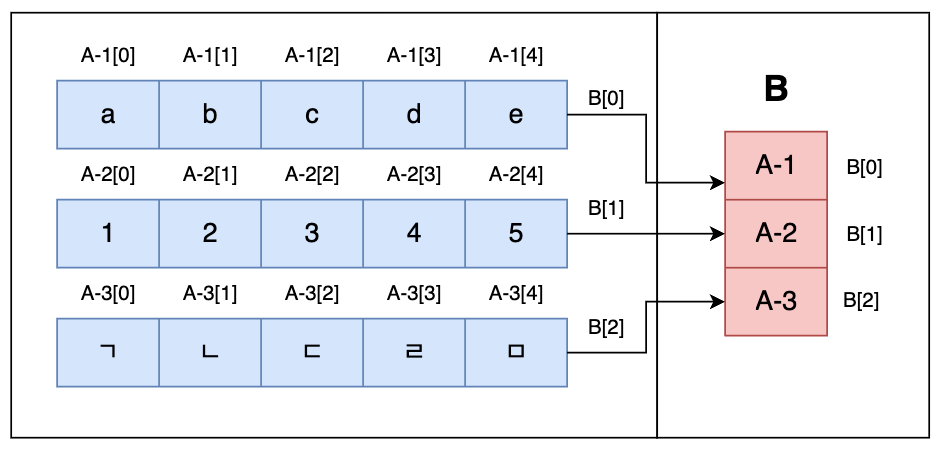
자세히 설명하자면, A-1, A-2, A-3 이라는 세 개의 배열이 있고, 이들을 각 원소로 가지는 B 라는 배열이 있는 형태이다. A-1, A-2, A-3 배열은 각각 B[0], B[1], B[2] 에 해당한다.
(2) 행렬과 행과 열
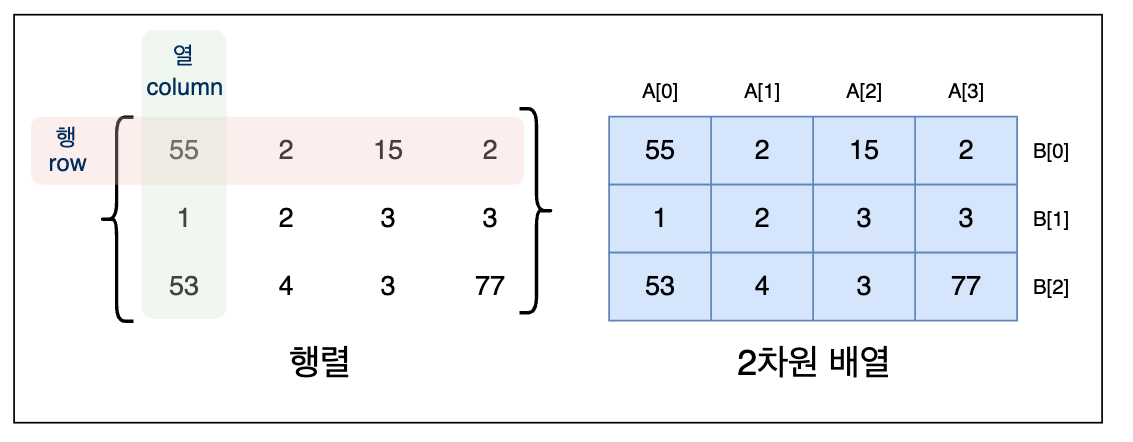
고등학교 수학시간에 행렬을 배웠을 것이다. 행렬을 컴퓨터에서 표현할 때에는 이와 같은 2차원 배열이 적합한다.
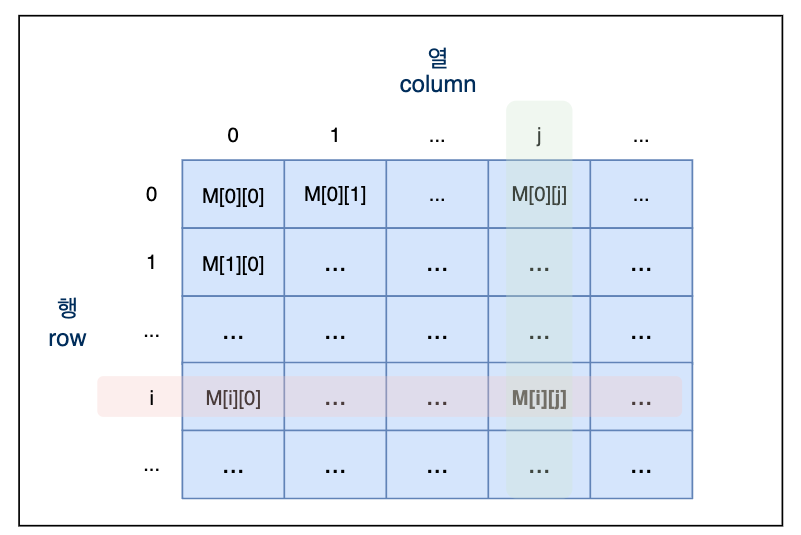
행렬에서는 가로 방향을 행, 세로 방향을 열이라고 부르며 2차원 배열이나 컴퓨터 과학에서도 동일하다. 행렬의 특정 원소를 지칭할 때에는 i행 j열에 위치한 원소에 대해 M[i][j] 라고 표현을 한다. 행 - 렬 이라는 이름과 동일한 순서임을 되짚어보면 기억하기 쉬울 것이다.
(3) 행 우선 메모리 할당과 행 우선 순서 행렬
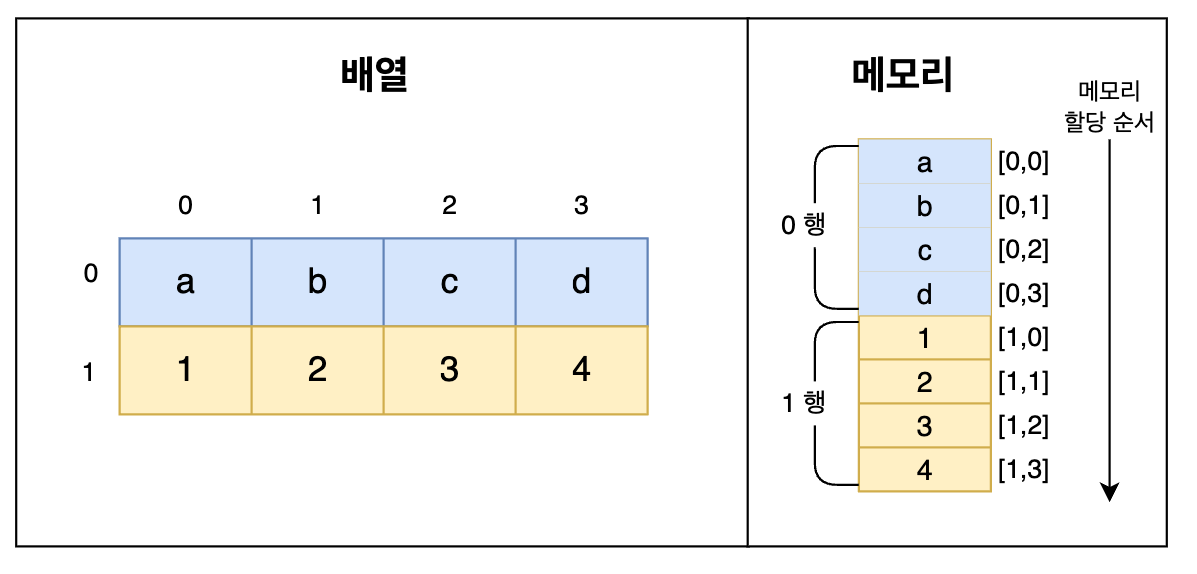
행 우선 메모리 할당이란 2차원 배열에서 행배열을 우선 메모리에 올리는 것을 뜻하며, 이 때의 행렬을 행 우선 순서 행렬 이라고 한다. 쉽게 말해 mxn 2차원 배열을 메모리에 올릴 때 0행의 0번 원소, 0행의 1번 원소 … 0행의 n번 원소까지 메모리에 올린 뒤, 이어서 1행의 모든 원소, 2행의 모든 원소, … m행의 모든 원소를 순서대로 메모리에 올리는 방식이다.
(4) 열 우선 메모리 할당과 열 우선 순서 행렬
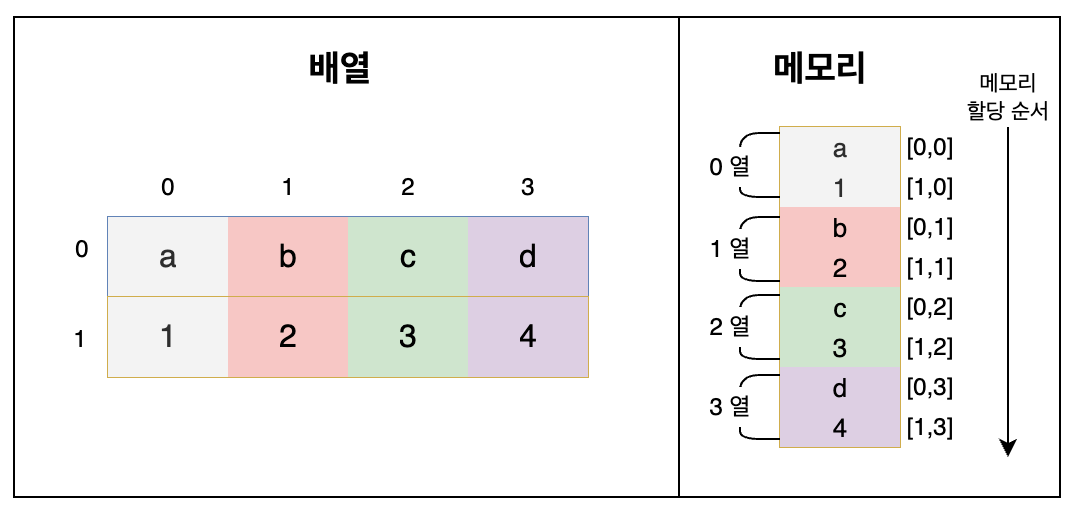
열 우선 메모리 할당은 2차원 배열에서 열 방향의 원소들을 먼저 메모리에 올리는 것이고, 이 때의 행렬을 열 우선 순서 행렬 이라고 한다. mxn 2차원 배열에서는 열 방향의 원소를 우선으로 하여 0열의 0번 원소(행), 0열의 1번 원소(행) … 0열의 m번 원소, 2열, 3열에 이어 .. n열의 m번 원소 순서로 메모리에 적재를 한다.
(5) 프로그래밍 언어에서의 행우선 배열과 열우선 배열
| 구분 | 행 우선 배열 | 열 우선 배열 |
|---|---|---|
| 프로그래밍 언어 | C, C++, Java, Python 등 | Fortran, MATLAB, R 등 |
| 정의 | - 2차원 배열을 메모리에 행 단위로 연속적으로 할당 | - 2차원 배열을 메모리에 열 단위로 연속적으로 할당 |
| 장점 | - 캐시 효율성 : 캐시 히트율이 높아짐 - 행 우선 접근 패턴시에 유리 |
- 열 우선 접근 패턴에 유리 |
| 단점 | - 열 단위 접근시 메모리 접근 분산으로 캐시 미스 발생 | - 대부분의 하드웨어와 언어가 행우선을 따르므로 일반적으로 비효율적 - 캐시 효율이 떨어질 수 있음 |
희소행렬
희소행렬의 정의
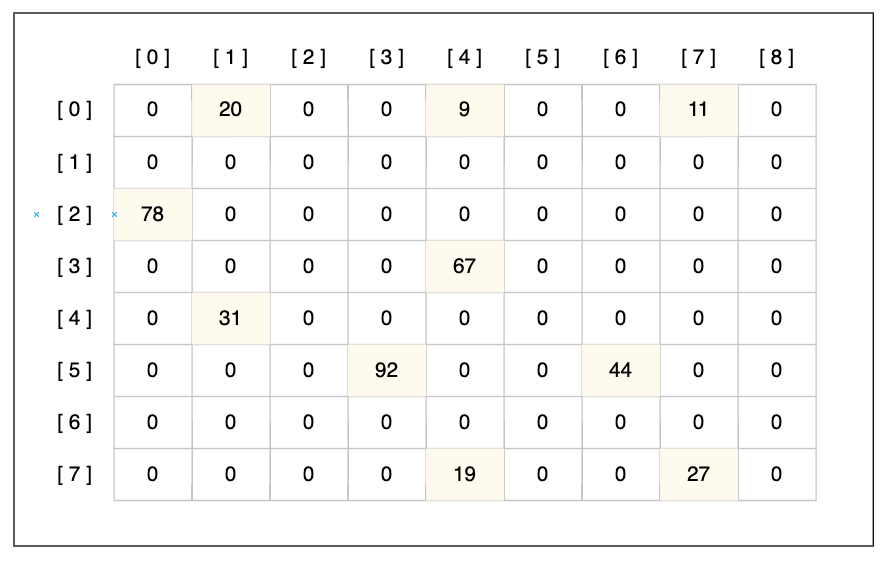
희소행렬은 행렬을 구성하는 원소들 중 값이 0인 원소의 수가 값이 0이 아닌 원소보다 상대적으로 많은 행렬을 의미한다.
sparse : 부족한, 희박한, 희소한
matrix : 행렬
희소행렬의 비효율성
희소행렬인 행렬을 컴퓨터에 저장할 때에는 원소의 많은 부분이 0으로 채워져 있기 때문에 0의 값을 저장하기 위해서 불필요하게 많은 메모리가 요구되는 비효율성이 발생한다. 따라서 희소행렬을 효율적인 방법으로 저장하는 방법에 대해 연구가 되었고, 값이 있는 원소에 대해 행과 열, 그리고 값을 차례대로 기입하는 2차원 배열 형태의 표현법이 등장하였다.
희소행렬의 효율적 배열표현
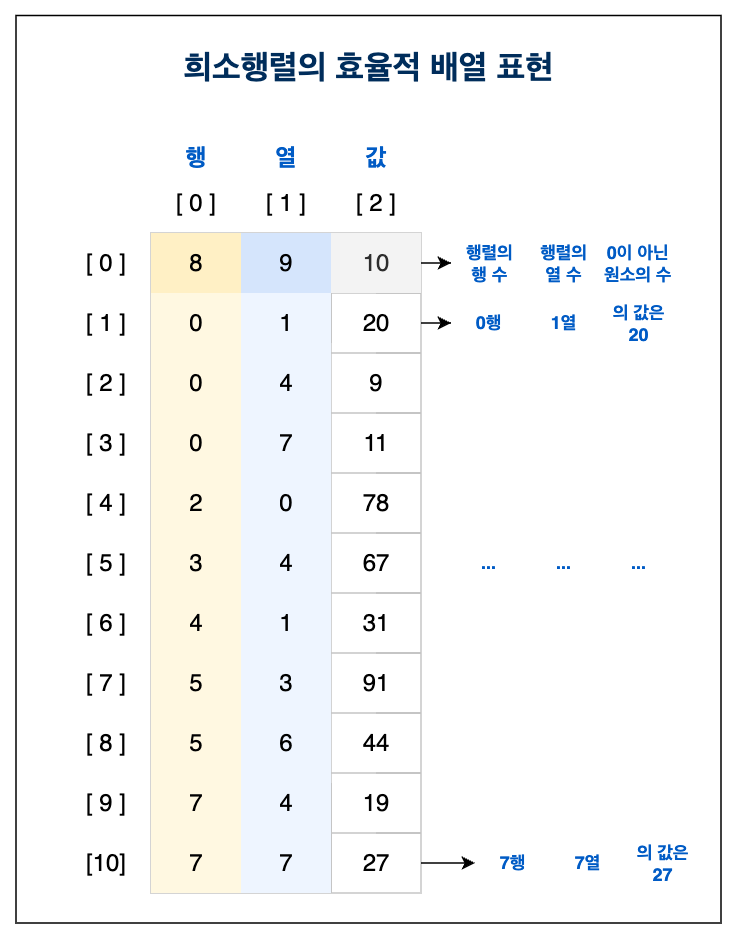
희소행렬의 효율적인 배열 표현은 위와 같은 3개의 열을 가진 2차원 배열 형태를 띈다.
-첫 번째 열은 행 번호를 의미한다.
-두 번째 열은 열 번호를 의미한다.
-세 번째 열은 해당 행x열 원소의 값을 의미한다.
-첫 번째 행은 순서대로 행렬의 행 수(크기), 행렬의 열 수(크기), 0이 아닌 원소의 개수를 의미한다.

Comments