차분배열 : 배열 구간 업데이트를 O(N)을 O(1)로 줄이는 방법

차분 배열

개념

• 차분배열, Difference Array
• 원본 배열의 $i$ 번째 원소와 $i-1$ 번째 원소의 차이로 이루어진 배열

핵심 원리

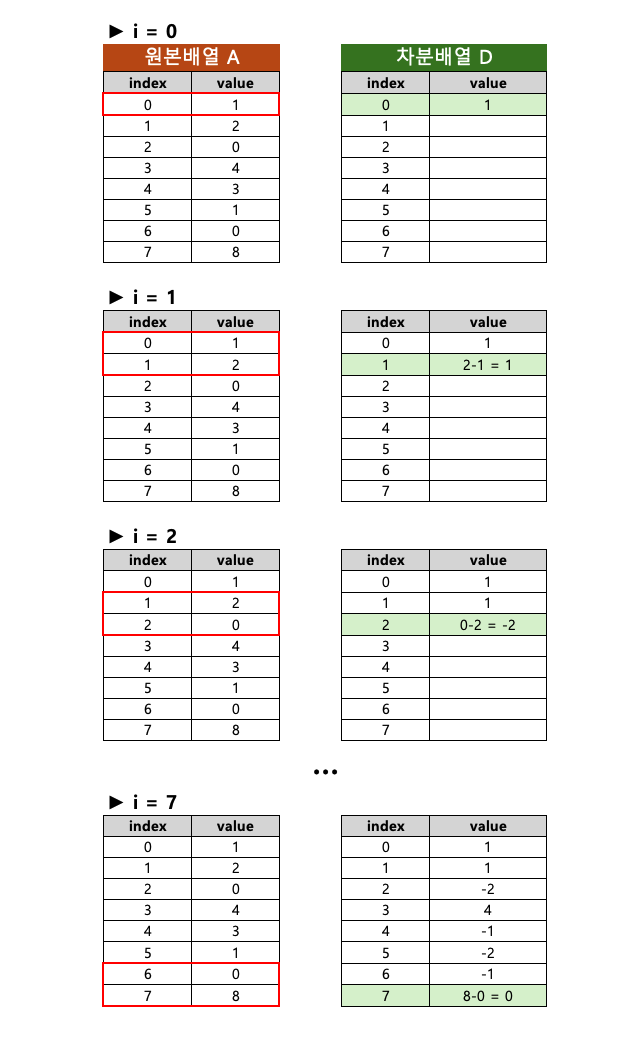
• 차분배열의 각 요소는 원본배열의 현재 요소와 이전 요소의 차이를 저장하는 배열이다.
• 원본배열 $A$ 에 대한 차분배열 $D$ 의 $i$ 번째 원소 $D[i]$ 는 아래와 같이 정의된다.

\[\begin{cases} i=0 & D[0] = A[0] \\ i > 0 &D[i] = A[i-1] \end{cases}\]

특징

• 배열의 특정 구간에 대한 값을 더하거나 빼는 구간 업데이트 작업을 효율적으로 처리
• 일반적으로 배열 $i$ 에서부터 $i+k$ 까지의 범위에 특정 값 $p$ 를 더하거나 빼려면 O(N) 의 시간복잡도
• 차분배열은 이러한 구간 업데이트 작업을 O(1) 시간복잡도로 처리할 수 있다.

예시

원본 배열 복원

• 앞에서부터 누적합(Prefix Sum)을 구하면 다시 원본 배열 $A$ 를 복원할 수 있다.

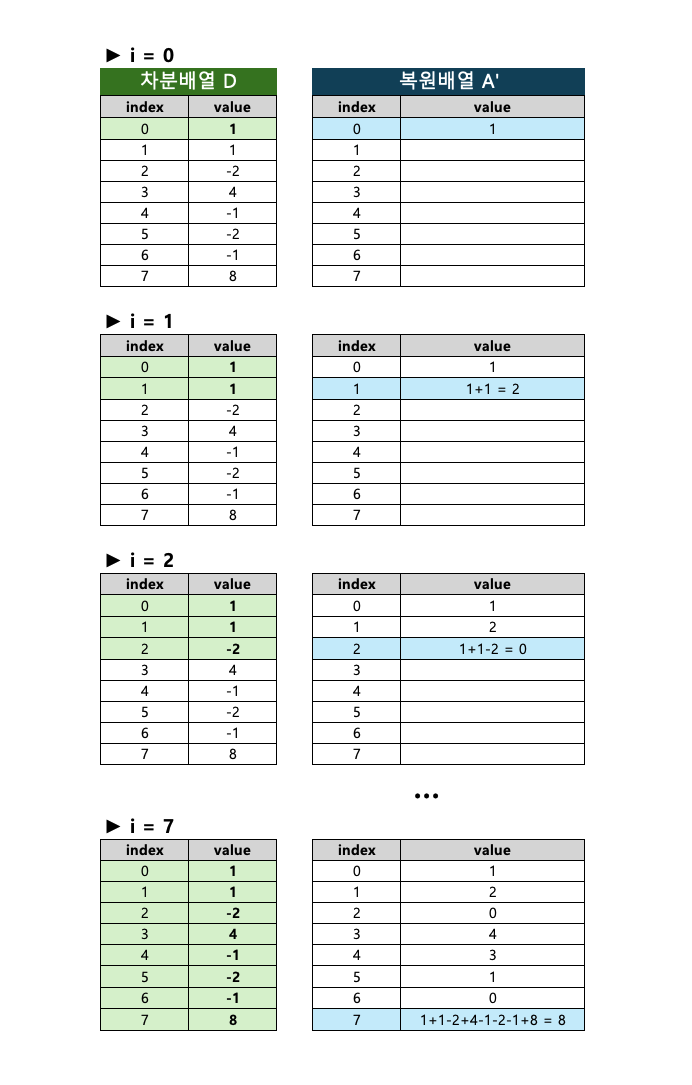
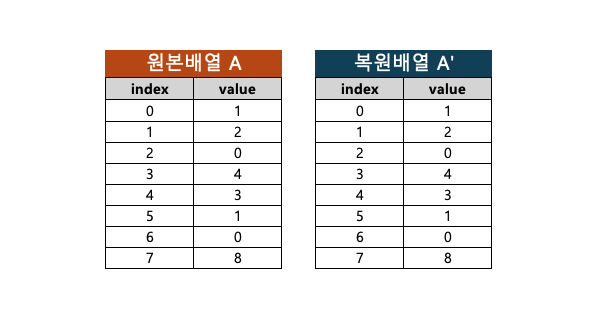
• 원본 배열과 복원 배열 비교

구간 업데이트 Range Update

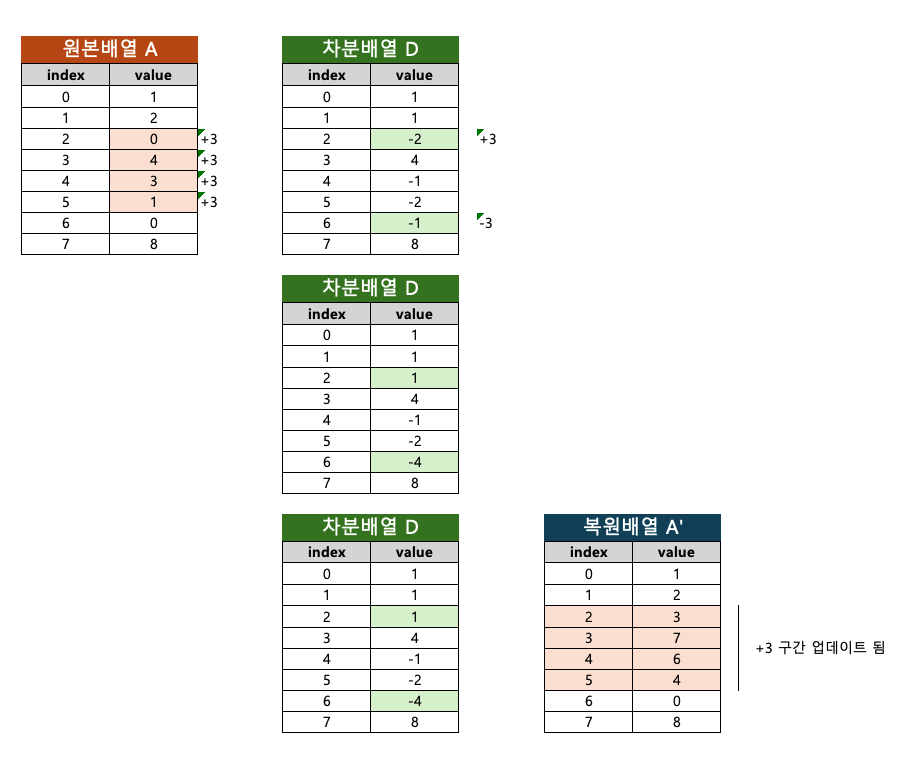
• 원본 배열 $A$ 의 $[i, i+k]$ 구간에 $p$ 라는 값을 더하고 싶을 때, 차분배열에서는 딱 두 지점만 수정하면 된다.

1. $D[i]$ 에 $p$ 를 더함 : $i$ 번째부터 그 이후의 모든 누적합 결과가 $p$ 만큼 증가한다.
2. $D[i+k+1]$ 에 $p$ 를 뺌 : $i+k+1$ 번째부터는 다시 원래의 값으로 돌아오도록 보정한다.

• 따라서 배열의 모든 요소를 반복시킬 필요가 없고, 딱 두 지점에 직접 접근하므로 O(1)의 시간복잡도를 가진다.

문제 풀어보기

https://whdrns2013.github.io/coding_test/20260109_001_server_expand/