선형변환에 의한 특징추출
선형변환
n차원 열벡터 x에 변환행렬 W(nxm)를 곱해서 m차원 특징을 획득하여 데이터의 차원을 축소하고, 분석에 불필요한 정보를 제거하는 특징추출 방법론이다. 영상이나 음성 신호, 텍스트 등 특성이 매우 다른 데이터들은 각각 그것에 맞게 설계된 특징추출 기법들이 존재한다. 선형변환은 그러한 데이터 특성에 의존하지 않고, 일반적인 데이터에 적용할 수 있다.
선형변환에 의한 특징추출의 목적은 (1) 차원 축소 (2) 분석에 불필요한 정보를 제거하는 것이며, 이 중 차원축소 목적이 가장 큰 목적이다.
선형변환은 n차원 열벡터 x에 변환행렬 W(nxm)를 곱해서 m차원 특징을 획득하여 데이터의 차원을 축소하고, 분석에 불필요한 정보를 제거하는 방향으로 진행된다.
2차원 데이터를 1차원으로 변형
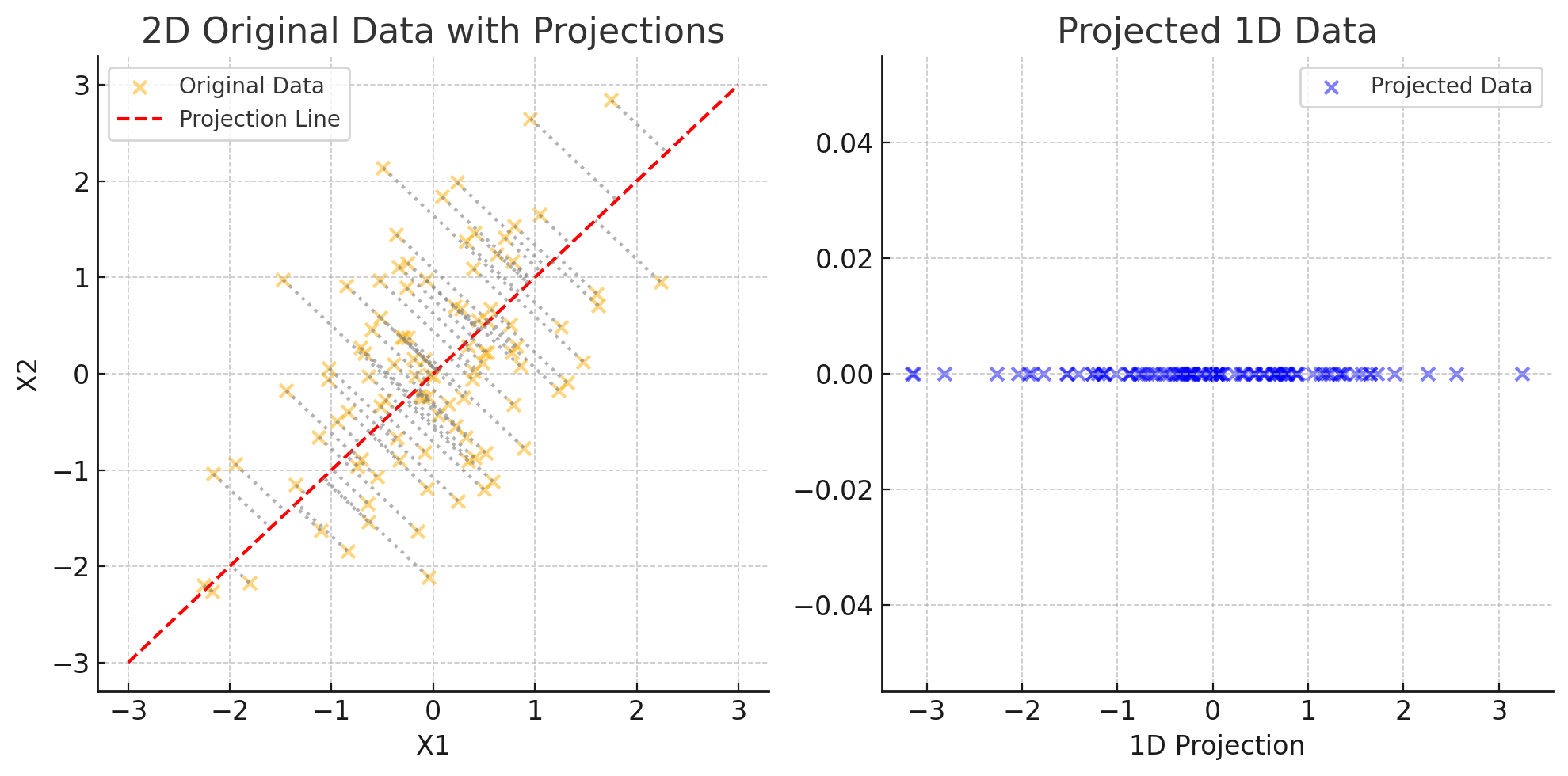
2차원 데이터를 1차원으로 변환하는 예를 그래프로 나타내보면 2차원 상에 특정 벡터에 대해 x축, y축 혹은 벡터 y의 위로 사영을 하는 것으로 표현할 수 있다.
예를 들어 [2, 2] 벡터 x에 대해 w = [1, 0] 위로 사영하는 것은 아래 그래프처럼 표현할 수 있다.
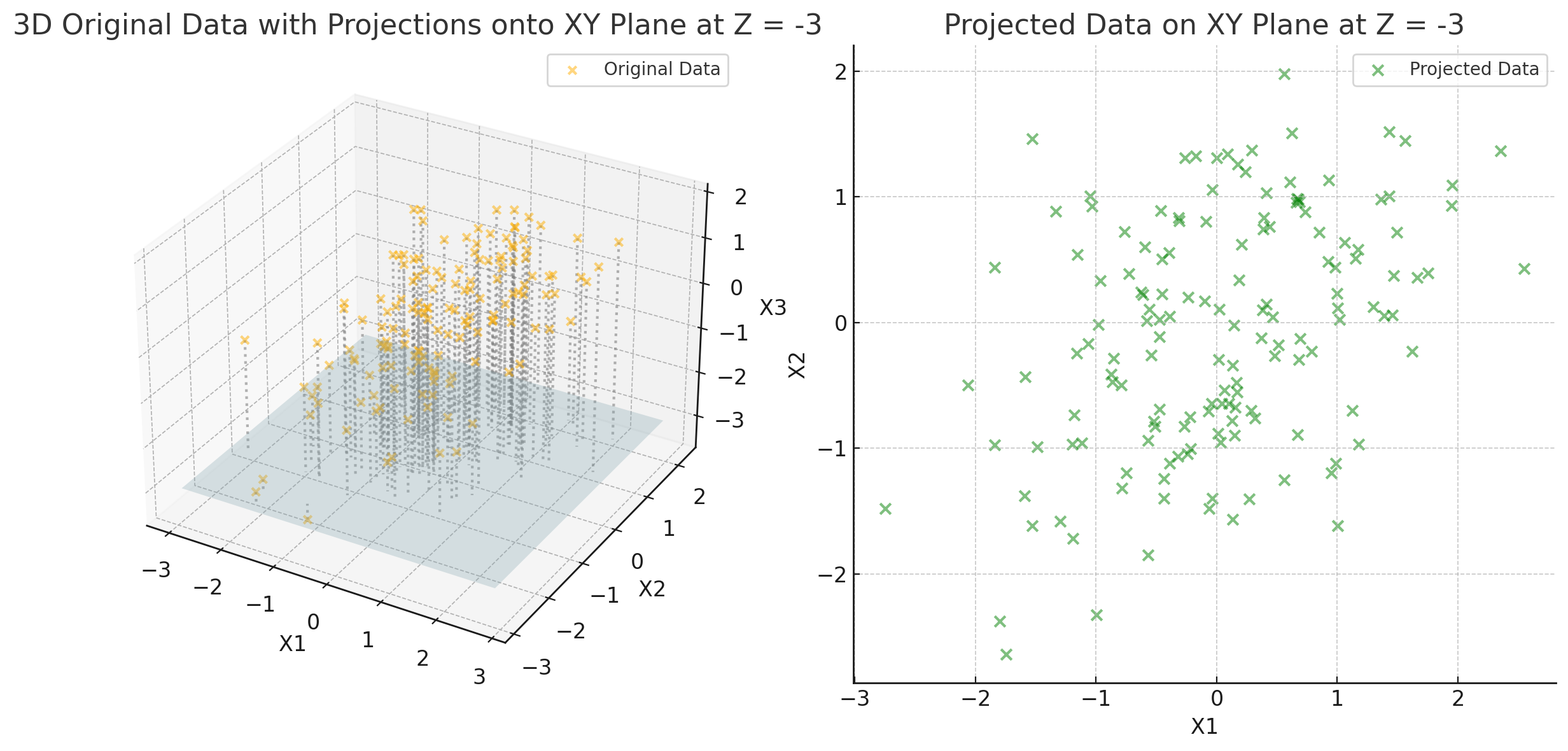
3차원 데이터를 2차원으로 변환
3차원 데이터를 2차원으로 변환하는 예를 그래프로 나타내면 3차원 상의 특정 벡터에 대해 특정 2차원 평변 위로 사영하여 2차원의 벡터(선)의 형태로 표현할 수 있다.
n차원 데이터를 m차원으로 변환
위에서 살펴본 바를 확장시켜 nxN 크기의 행렬 X=[x1, x2, x3 … xN]에 대한 변환행렬 W의 특징 추출 과정은 아래와 같은 식으로 정리할 수 있다.
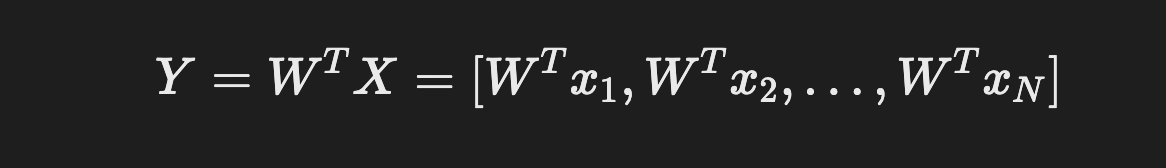
그리고 변환행렬은 아래와 같이 정리할 수 있다.
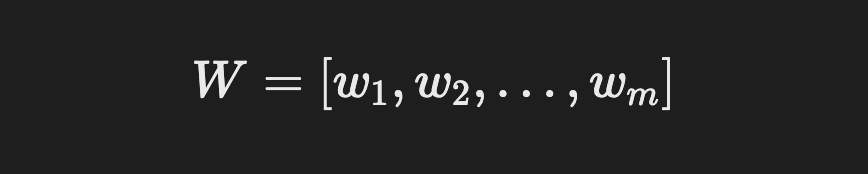
변환행렬에 따른 특징추출 형태
변환행렬에 따라 특징추출의 결과는 많은 차이를 보일 수 있다. 쉽게 이해하게끔 하려면, 3차원 데이터를 어떠한 2차원 평면에 나타내는지에 따라 아래와 같이 결과 데이터의 분포가 많이 달라지고, 모델의 성능이 좌우된다. 때문에 사영할 적절한 2차원 평면을 결정하는 변환행렬 W를 찾는 것이 매우 중요하다.
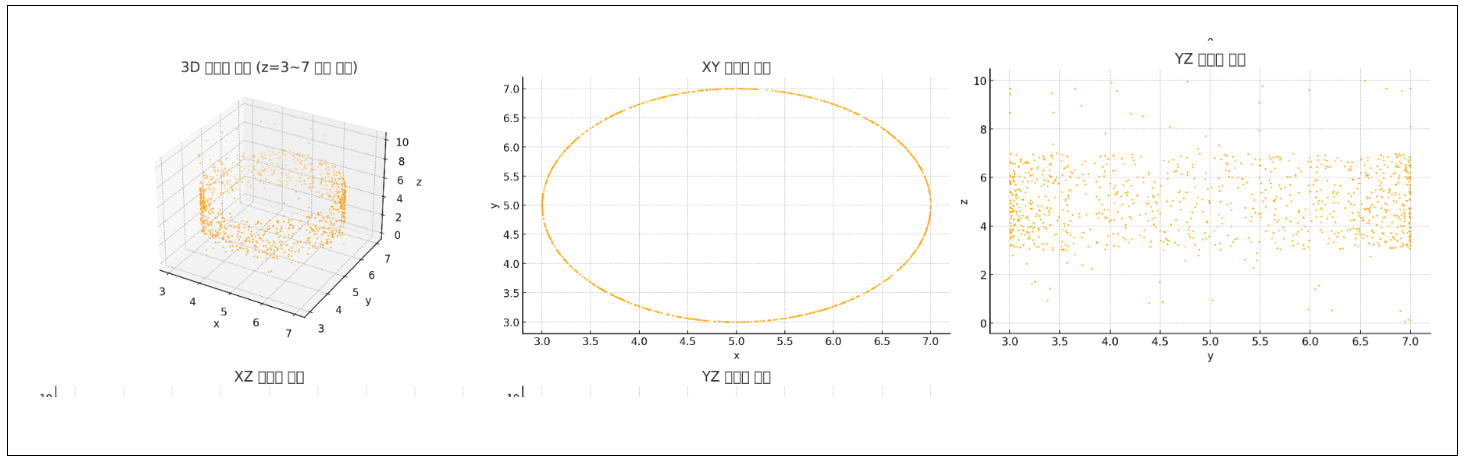
좋은 특징추출이란?
분석 목적에 맞는 특징 분포를 만드는 과정이다. 이를 위해 변환행렬 W를 적절히 조절해서 데이터의 중요한 정보는 보존하고, 불필요한 정보는 제거해야 한다.
변환행렬 W에 의해서 변환되는 데이터의 형태가 많이 달라지므로, W가 무엇을 기준으로 설계되었는지에 따라 특징 추출의 결과물과 성능이 많이 달라지게 된다. 이 때 적젏한 변환행렬 W를 찾기 위해 사용하는 기법으로 주성분 분석(PCA), 선형 판별 분석(LDA), 독립성 분석(ICA) 등이 있으며, 분석 목표에 따라 적절한 방법을 택한다.
이 중 통계적인 추출 방법은 주성분분석과, 선형판별분석이 있으며 다음 포스팅부터 다뤄보도록 한다.
대표적인 통계적 특징추출 방법
| 통계적 특징추출 방법 | 설명 |
|---|---|
| 주성분분석법 | 클래스 정보를 사용하지 않는 비지도 학습법 |
| 선형판별분석법 | 클래스 정보를 사용하는 지도 학습법 |

Comments