로지스틱 회귀
로지스틱 회귀란
선형회귀의 종속변수(출력값)를 실수형 숫자값이 아닌, 범주형으로 확장한 것을 의미한다. 0 과 1 사이의 확률값을 출렿가는 로지스틱 함수를 이용한 회귀 방법으로, 주로 두 클래스 중 어느 클래스에 속할지 판단하는 이진 분류문제에 사용되며, 특정 사건이 발생할 확률을 예측하는 데 활용된다.
로지스틱 함수
로지스틱 함수는 시그모이드 함수의 일종으로, 인구 성장 모델을 설명하기 위해 도입한 ‘로지스틱 곡선’에서 비롯된 함수이다. 로지스틱 곡선은 초기에는 지수적으로 증가하지만, 성장률이 감소하면서 결국 포화상태에 도달하는 S자 형태를 나타낸다.
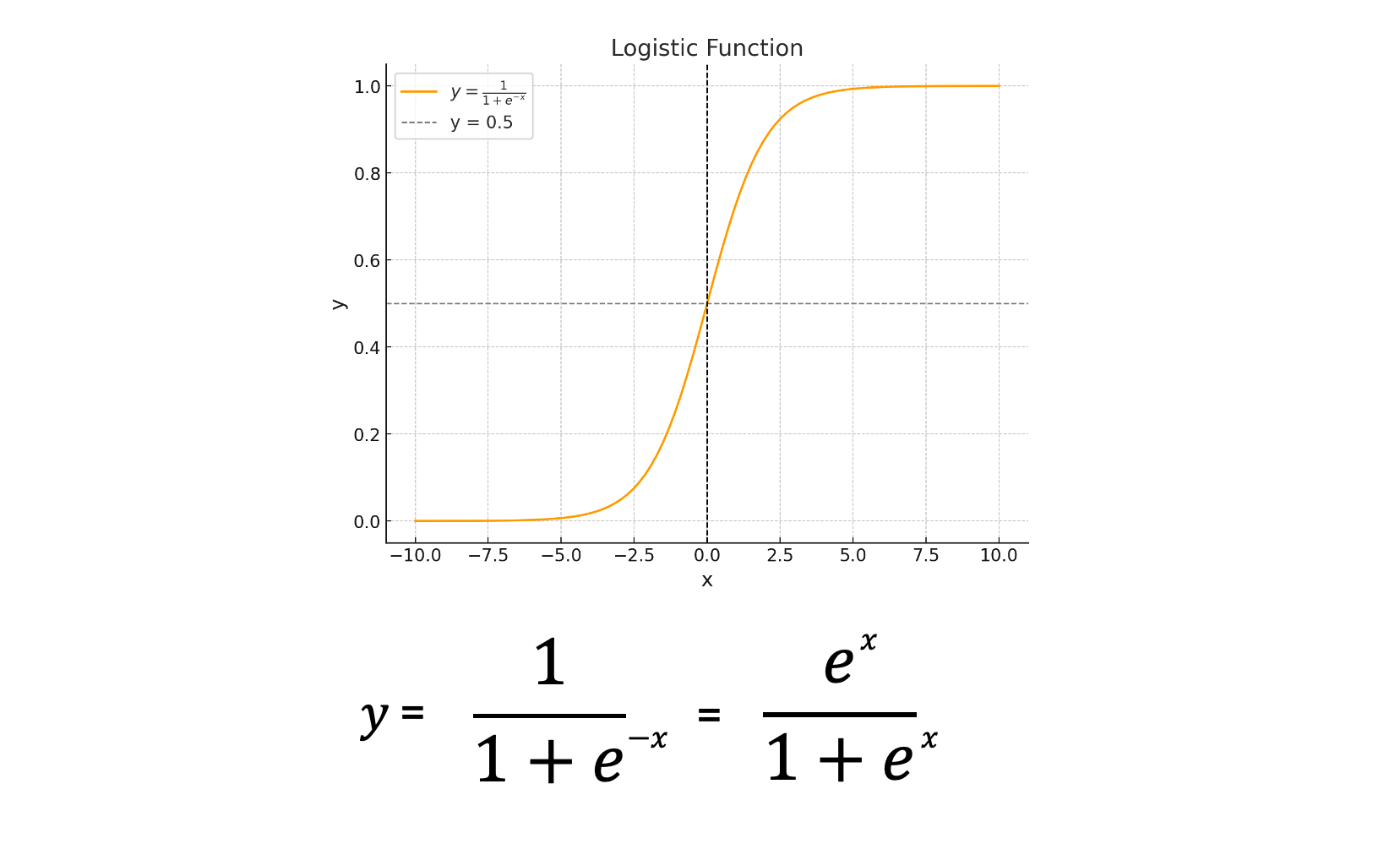
로지스틱 회귀 함수
위 로지스틱 함수는 입력값 x가 주어졌을 때 클래스 레이블이 1 클래스에 속할 조건부 확률이 출력값이 된다. 따라서 입력값 x를 선형함수 f(x)=mx + b 로 바꾸면 입력값 x에 대해 출력값이 클래스 1에 속할 확률 을 구할 수 있는 것이다.
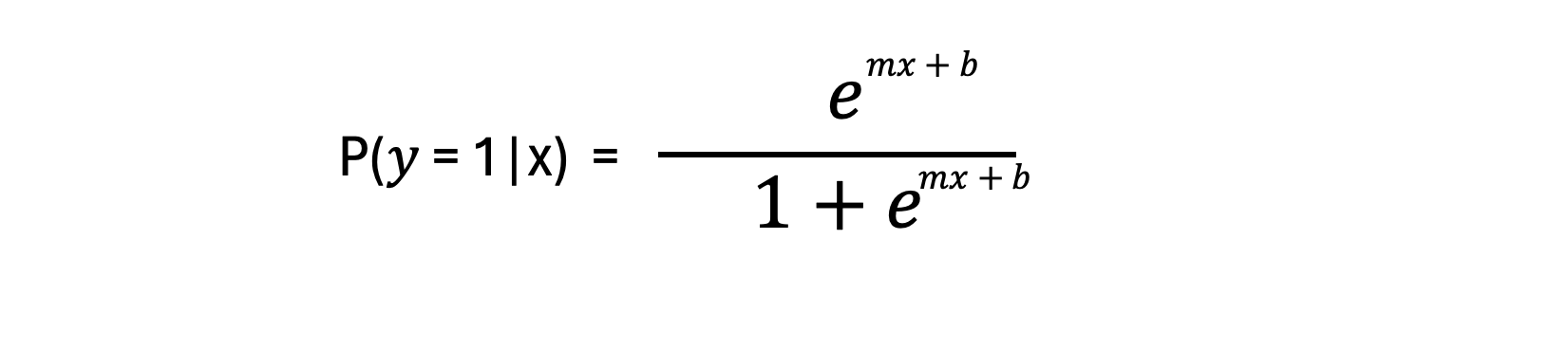
이 로지스틱 함수에 대해 P(y=1|x)의 값이 0.5 이하이면 입력값 x에 대한 데이터는 C1 클래스에 속하고, 반대로 0.5 이상의 출력값이 나온다면 데이터는 C2 클래스에 속하게 된다.
출력값과 로지스틱 함수의 모양은 선형함수의 기울기 m과 절편 b에 의존적이며, 이 두 값의 변화에 따른 그래프 예시는 아래와 같다.
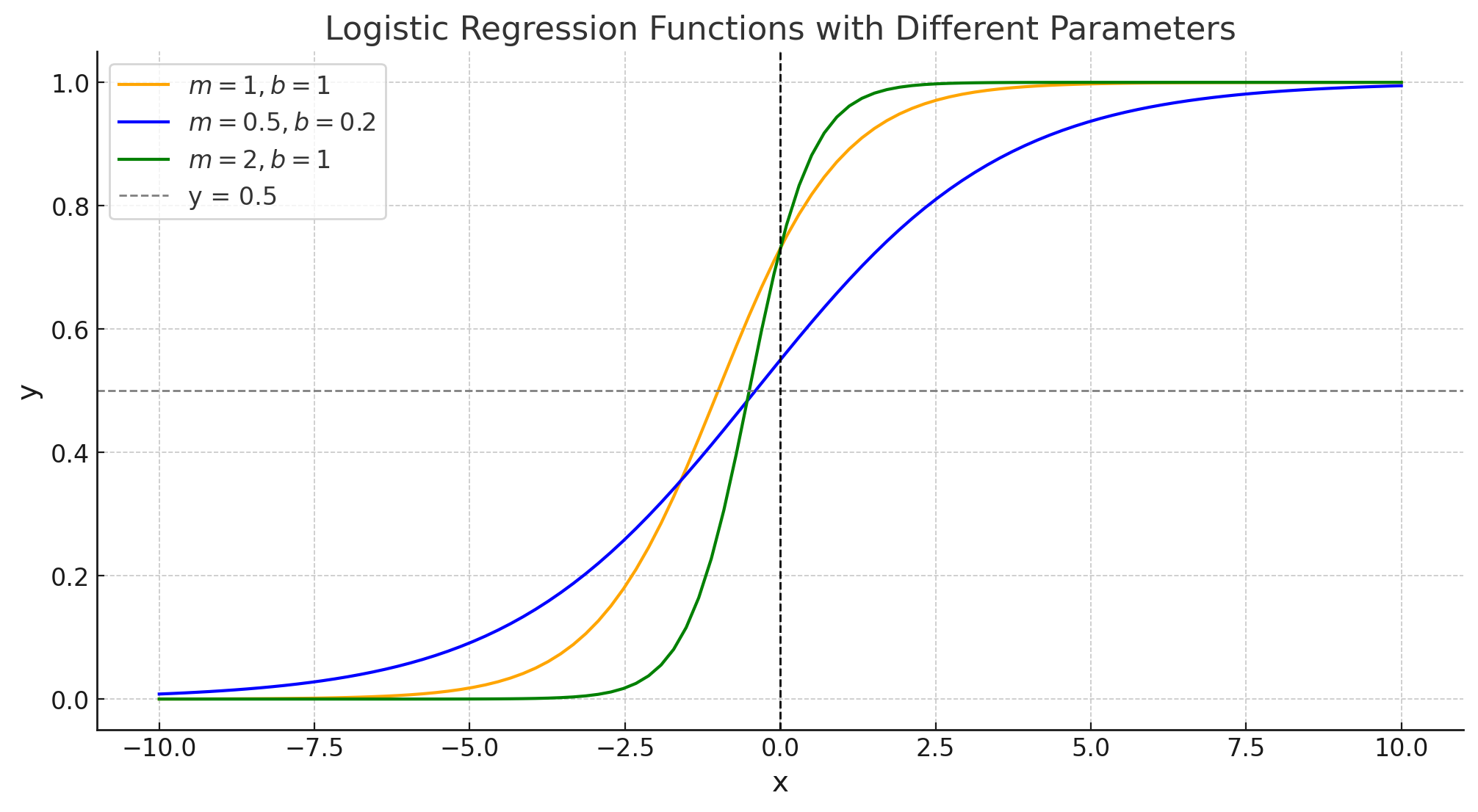
로지스틱 회귀 매개변수 추정 방법
로지스틱 회귀의 중심 개념
(1) 오즈비
오즈비(odds ratio)란 두 가지 사건의 발생 가능성을 비교하는 데 사용하는 측정값으로, 사건이 발생할 확률과 발생하지 않을 확률 간의 비율을 뜻한다. 즉 오즈비의 값이 1이면 사건이 발생할 확률과 발생하지 않을 확률이 같은 것이고, 오즈비가 1 초과면 사건이 발생할 가능성이 더 큰 것임을 의미한다.

| 그리고 여기서 P(y=1 | x)에 대해 앞서 살펴본 로지스틱 회귀 함수 정리를 대입하면 아래와 같이 정리할 수 있다. |
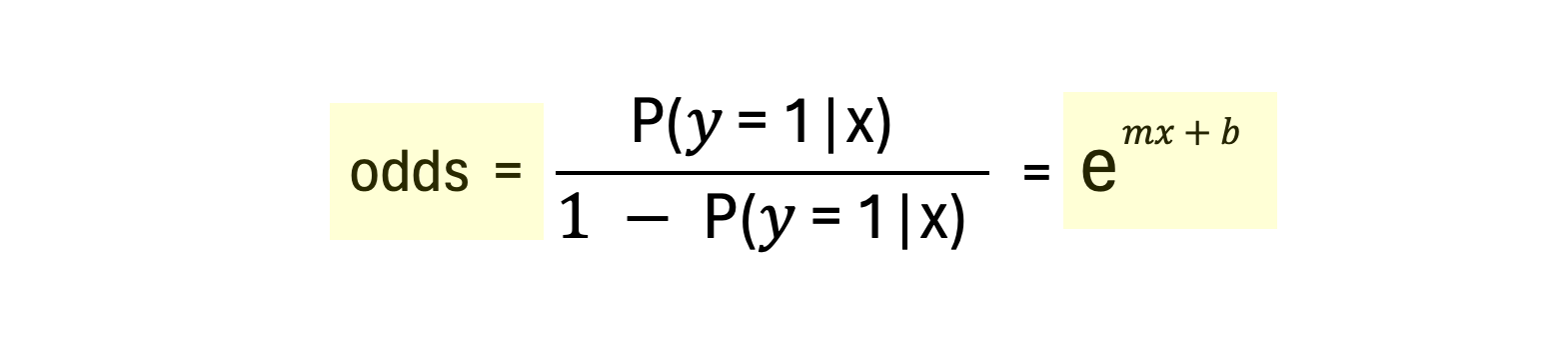
(2) 로짓 함수
로짓 함수는 오즈비를 자연로그로 변환한 함수를 뜻한다. 자연로그를 취하는 이유는, 확률을 선형화하여 선형 회귀 형태로 표현하고 회귀함수에 대해 해석을 용이하게 할 수 있게 해주기 위함이다.
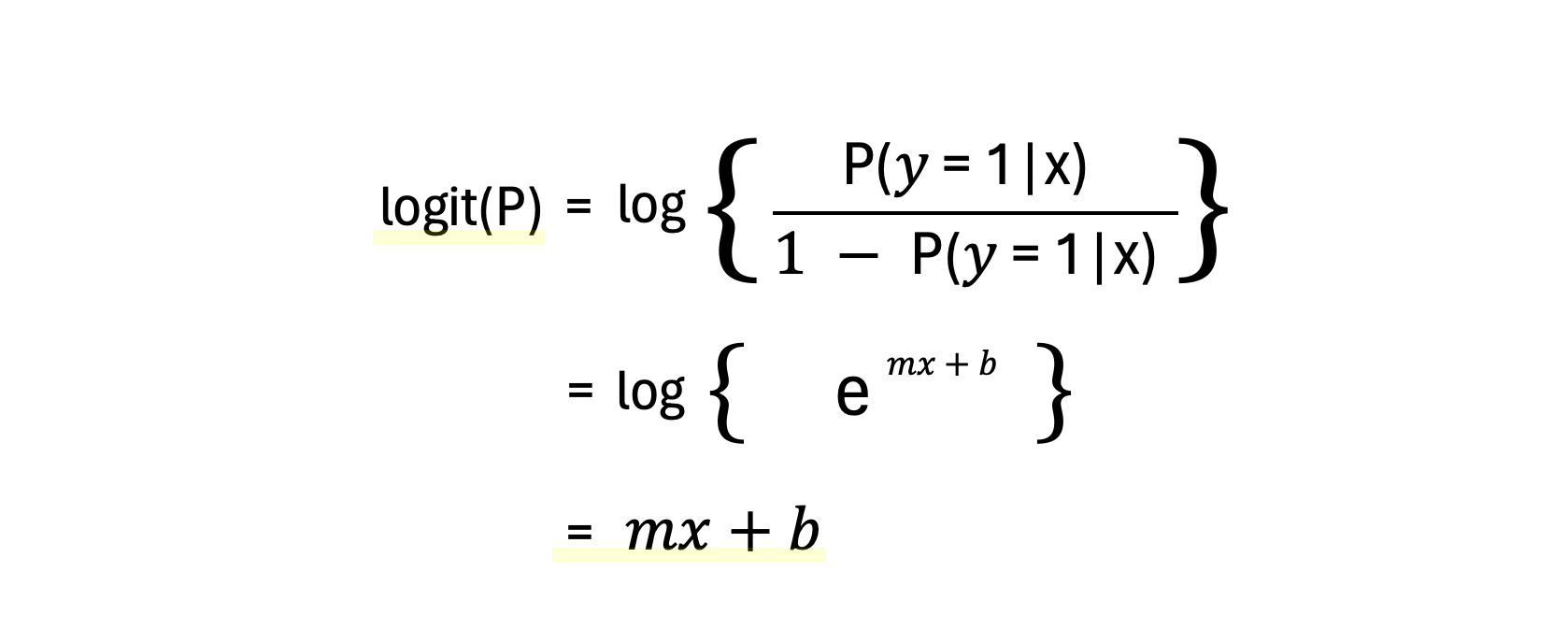
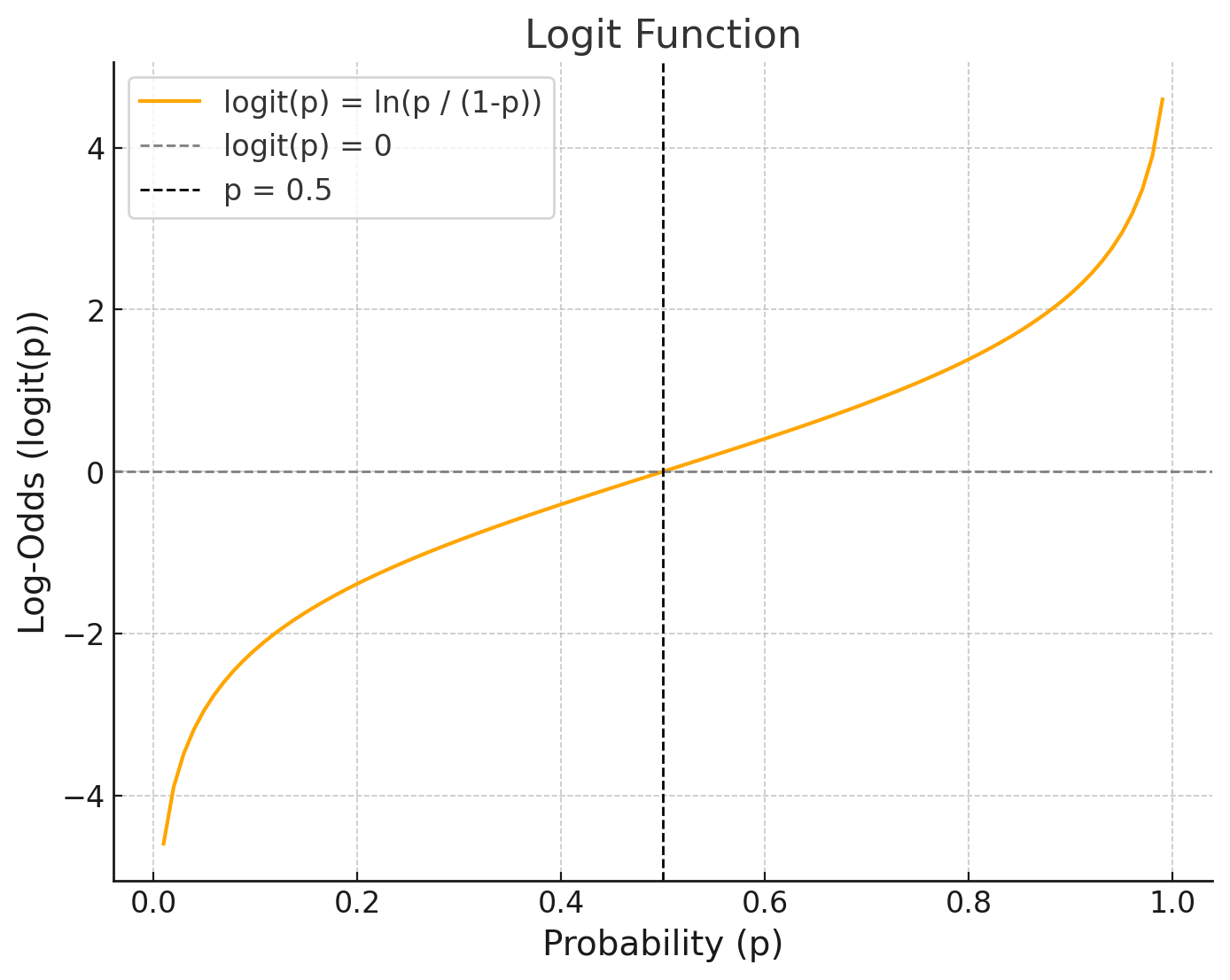
(3) 로지스틱 회귀의 결정 경계
이 로짓 함수를 이용한 판별함수는 로짓함수 = mx+b = 0인 선이 된다. 따라서 최적의 판별함수를 찾기 위해서는 파라미터 m과 b의 최적값을 찾으면 되는 것이다.
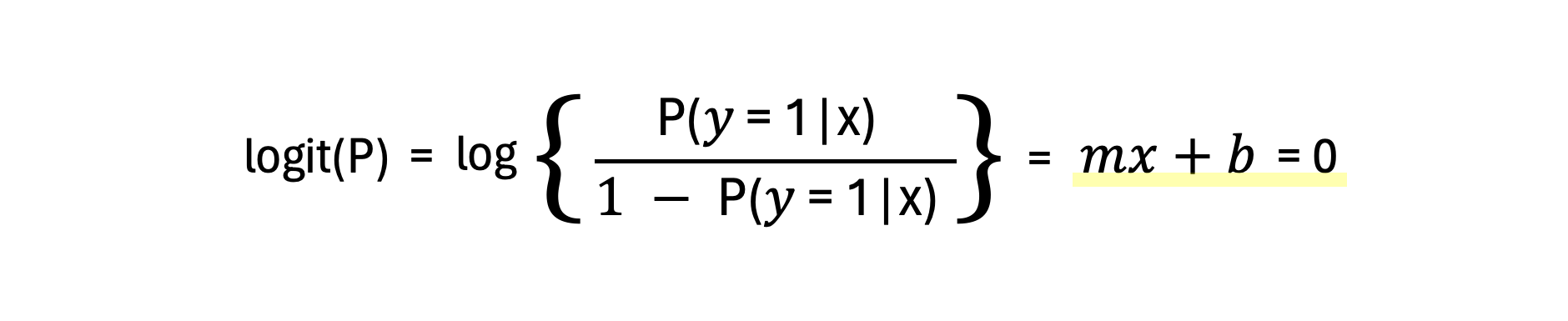
로지스틱 회귀에서의 오차 측정
일반적인 선형 회귀함수였다면 실제값 - 예측값을 오차로 정의할 수 있지만, 로지스틱 회귀함수는 1과 0 사이의 확률값을 출력하므로, 새로운 오차 측정 방법을 정의해야 한다. 로지스틱 회귀함수에서의 오차를 최소화한다는 것은 실제값의 클래스일 확률을 최대화하는 출력을 내는 것으로 정의할 수 있다. 이것은 데이터에 대한 로그 우도를 최대화 하는 최대 우도 추정법을 통해 파라미터를 추정하는 것으로 수행할 수 있다.
로그 우도
데이터 집합 D = {(xi, yi)}, i = 1, 2, 3 ... N 에 대해 P(y |
x)의 확률함수는 베르누이 분포를 따르므로 다음과 같이 나타낼 수 있다. |
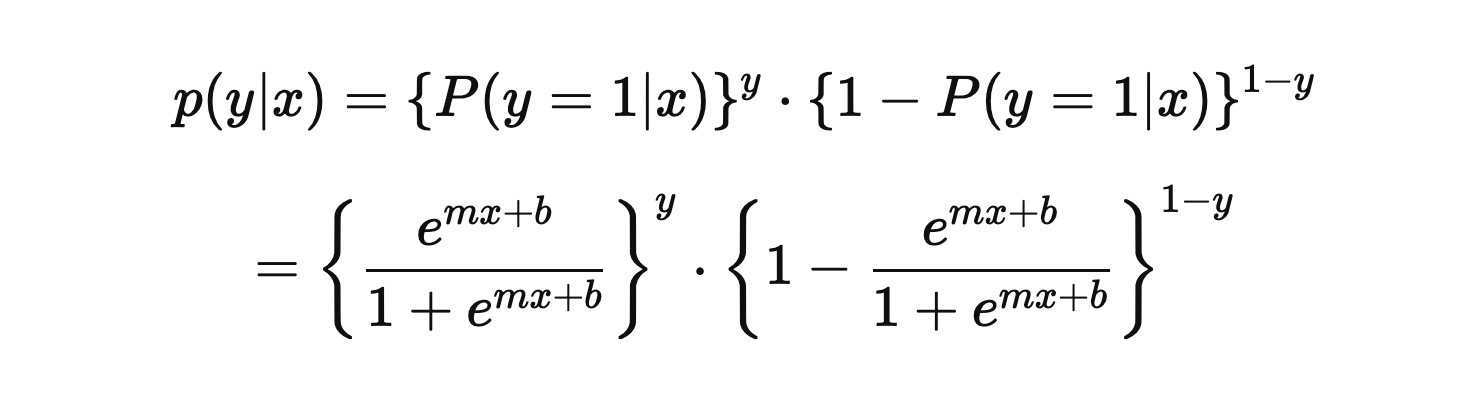
이어서 데이터 집합 D에 대한 로그 우도는 다음과 같이 정의한다.
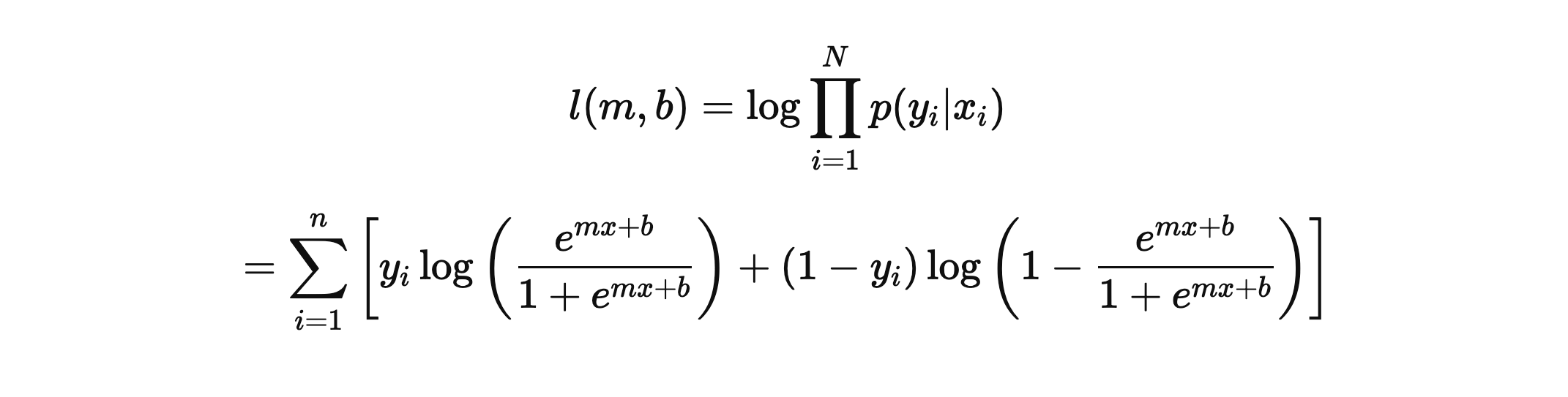
최대 우도 추정법
최적의 파라미터를 추정하기 위해서는 로그 우도를 편미분한 연립방정식의 해를 찾는 문제로 귀결된다.
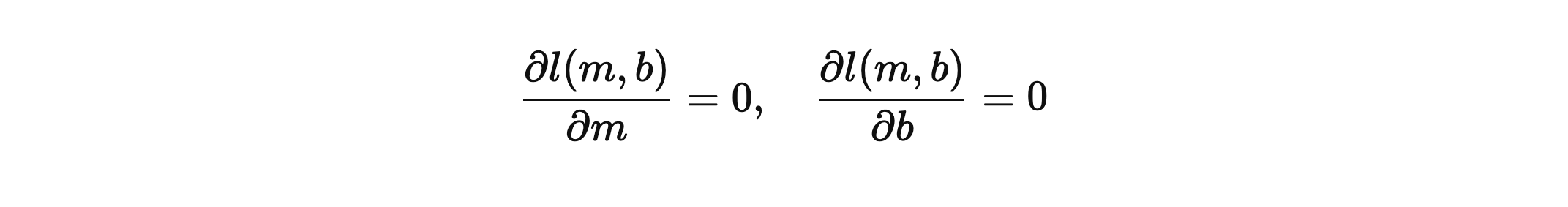
하지만 로그 우도식은 초월함수를 포함하는 복잡한 비선형 함수로, 위의 로그 우도를 편미분한 연립방정식의 해를 간단하게 얻는 것은 불가능하기 때문에, 이 경우엔 수치적 최적화 방법으로 반복적 추정을 통해 해를 찾아가야 한다. 이를 위한 대표적인 방법은 신경망 학습에서 사용되는 기울기 강하 학습법이 있다.(이번 포스팅에서는 생략, 추후 설명)
로지스틱 회귀의 우도 추정법
최대 우도 추정법을 통해 최적의 m과 b의 값이 얻어지면, 새로운 데이터 xnew에 대해서는 아래와 같은 판별식을 만들 수 있다.
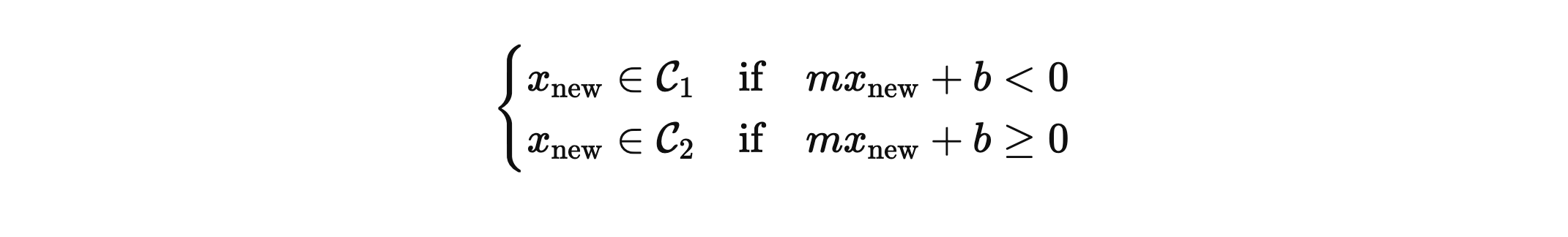

Comments