다변량 선형 회귀
개념
- 다변량 : 입력값 x 가 여러 개의 값(특징)으로 이루어진 경우
- 선형 회귀 : 입력값 x와 출력값 y 간의 매핑 함수
- ex. 입력값 : 나이, 몸무게 / 출력값 : 수축기 혈압
초평면 (hyperplane)
- 초평면이란 기하학에서 n차원 공간에서의 n-1차원 부분 공간을 의미하는 단어이다.
- 예를 들어 3차원에서의 초평면은 2차원 평면 형태가 될 것이다.
- 2차원에서의 초평면은 1차원인 선 형태가 될 것이다.
- 1차원에서의 초평면은 0차원인 점 형태가 될 것이다.
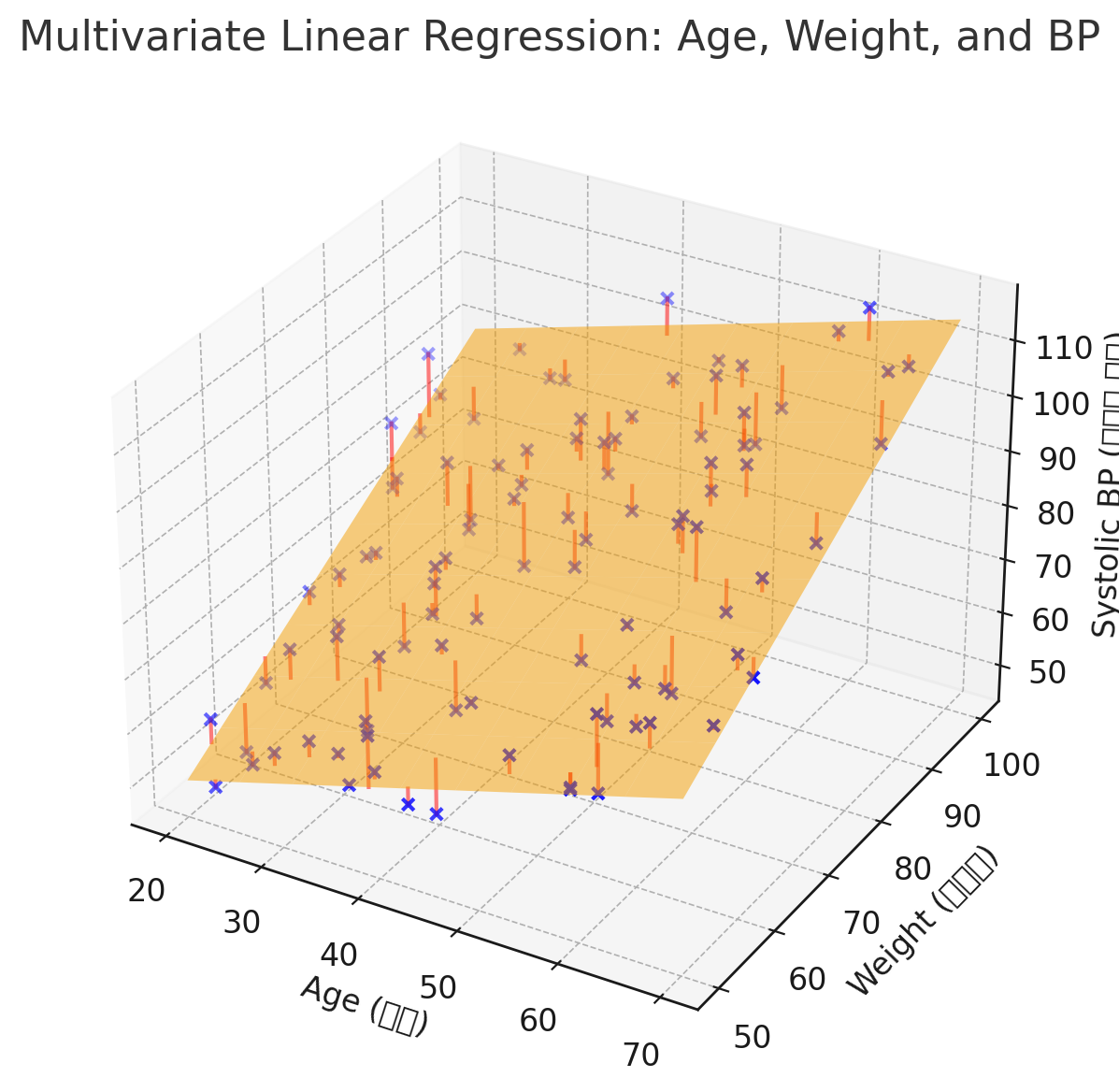
그래프에서의 다변량 선형 회귀 표현
- 단변량 화귀함수 (입력값 x 가 한 종류인 선형회귀)의 경우 입력값 x와 출력값 y 를 그래프로 표현하면 직선 형태가 된다.
- 입력값이 2가지 종류인 경우(이변량) x0, x1, y 세 가지가 그래프로 표현되고, 이때의 회귀함수는 평면으로 표현된다. (아래 예시)
- 결론적으로 다변량 회귀함수는
f(x) = w0 + w1x1 + w2x2 + ... + wnxn으로 나타낼 수 있으며, 그래프에서 n+1차원(x개 + 출력값 1개) 공간에서의 n차원 부분공간(초평면으)로 나타난다.
다변량 선형 회귀의 행렬 표현과 최적해 구하기
다변량 선형 회귀의 행렬 표현
다변량 선형 회귀, 즉 n개의 변수와 상수값(절편) 으로 이루어진 함수를 효율적으로 다루기 위해 행렬 형태 식으로 표현할 수 있다.
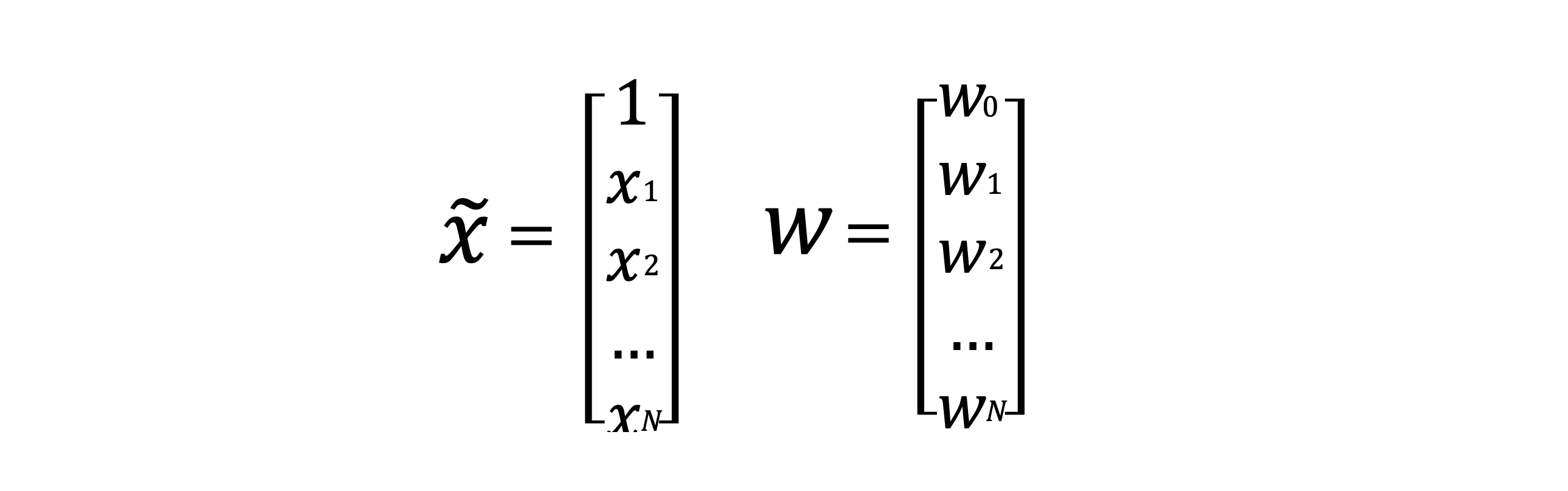
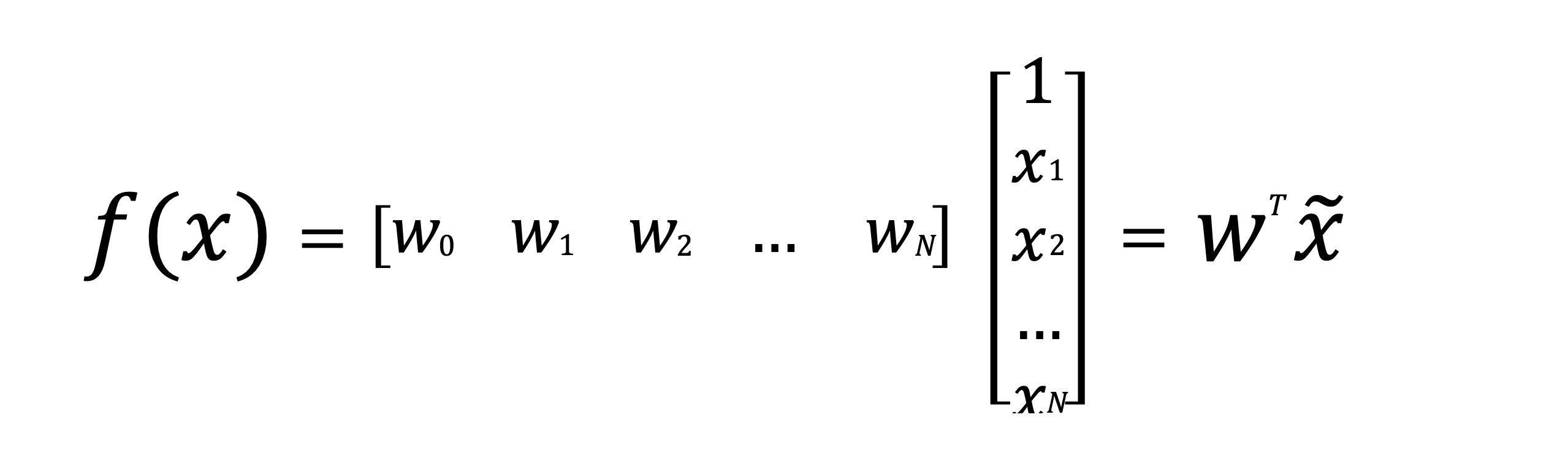
이에 대한 오차함수와, 최적의 w 행렬을 구하기 위해 편미분한 수식은 아래와 같다.
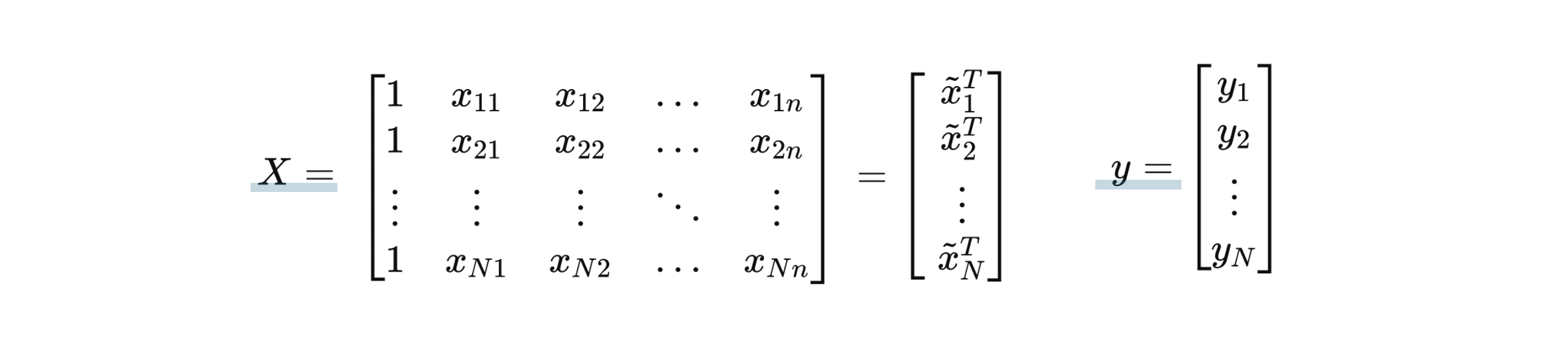
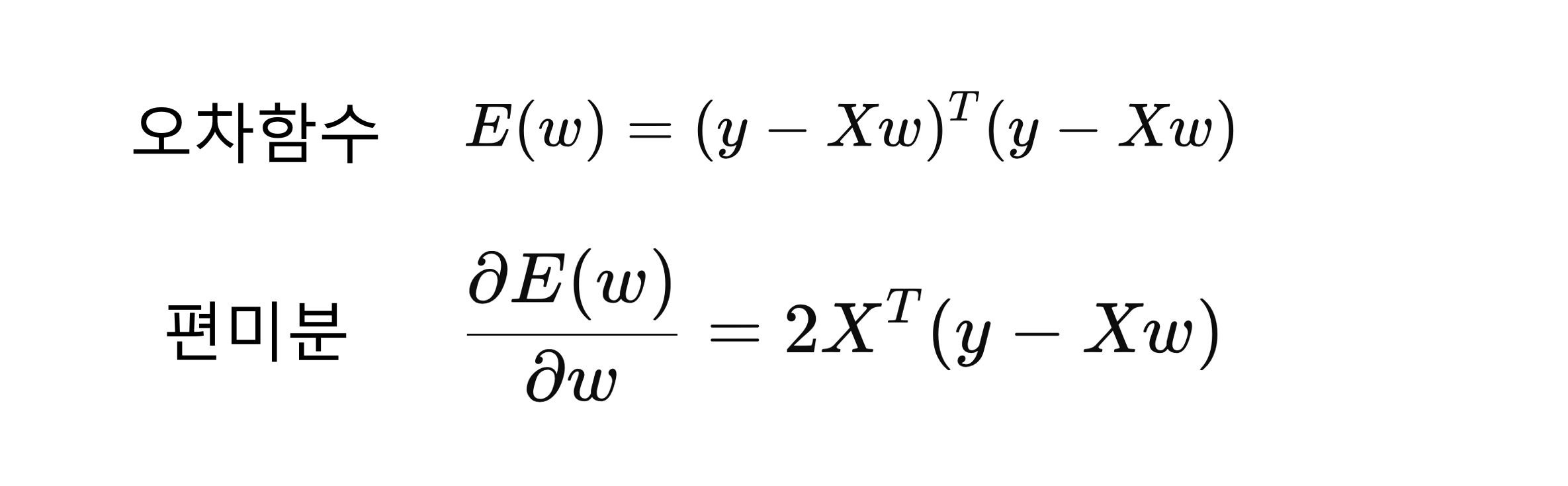
편미분한 식을 정리하면
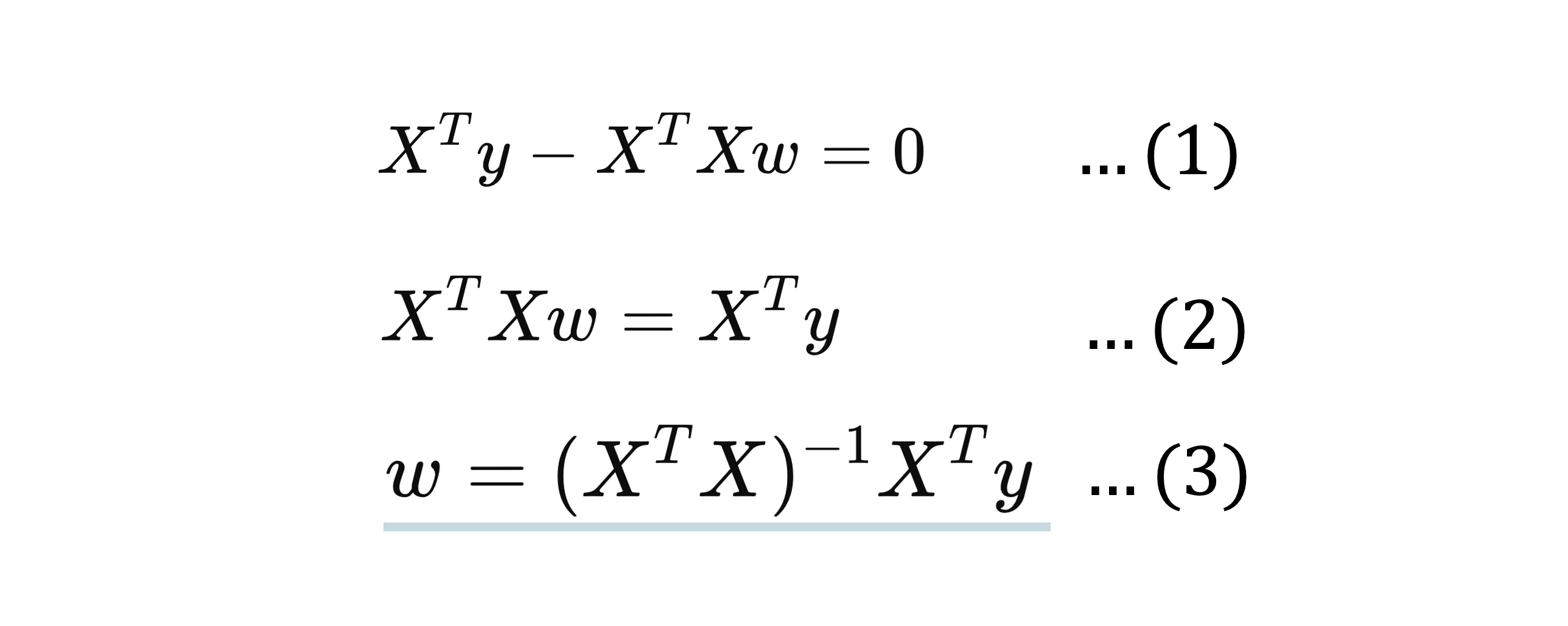
이 식에서 X와 y는 데이터로부터 얻을 수 있기 때문에, 최적 파라미터 w의 값을 얻을 수 있다.

Comments