선형회귀의 개념
선형회귀란
입력(또는 독립변수)과 출력(또는 종속변수) 쌍의 데이터의 관계를 설명하는 모델(혹은 함수)이 선형(직선 형태)인 분석 방법을 뜻한다. 입력(x)과 출력(y)가 선형이라는 것은, y = w1x + w0 + e 형식의 일차식 형태라는 말과 동일하다.
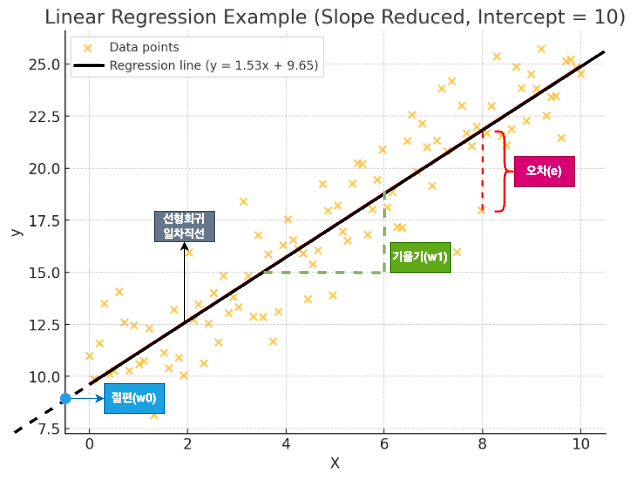
| 요소 | 설명 |
|---|---|
| y | 출력값 |
| x | 입력값 |
| w1 | 기울기 |
| w0 | 절편 |
| e | 오차 |
즉 선형회귀 분석을 한다 또는 선형회귀 모델을 만든다는 것은 입력값 x와 출력값 y를 매핑하고, 예측값과 실제값의 오차를 최소화하는 기울기 w1과 절편 w0을 구하는 것이라고 정히할 수 있다.
오차함수
앞서 설명한 선형회귀에 대한 개념 설명을 기반으로 좋은 선형회귀 모델이란, 실제값과 예측값의 차이 즉 오차가 작은 모델이라고 정의할 수 있다. 따라서, 좋은 모델을 만들기 위해서는 오차를 계산할 수 있어야 한다.
어떠한 하나의 입력 데이터에 대한 오차는 이전 섹션에서 정리한 바에 따라 e = y - w1x -w0 라고 할 수 있으며, 전체 데이터에 대한 오차는 아래와 같이 나타낼 수 있다.
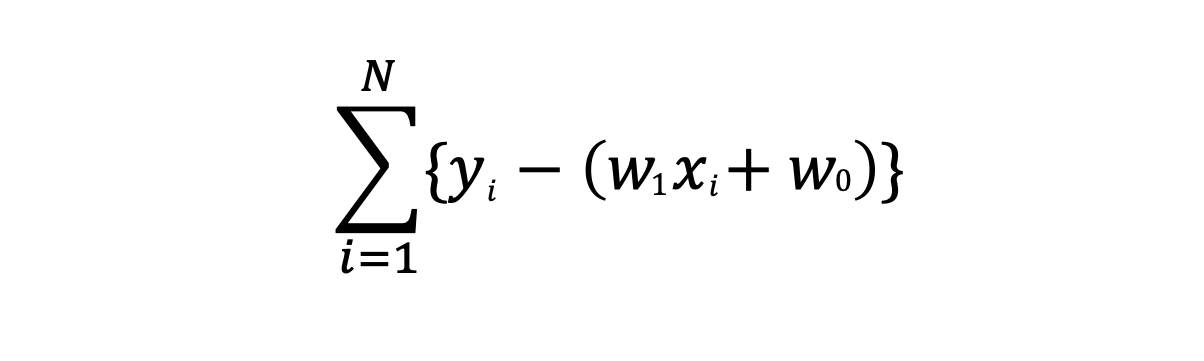
하지만 오차는 양수일수도, 음수일 수도 있으므로 위 식을 적용하면 양수와 음수가 상쇄되면서 제대로 된 오차를 계산할 수 없다. 따라서 일반적으로 오차에 대한 제곱값을 모두 더하는 평균 제곱 오차(Mean Squared Error:MSE)를 사용한 오차함수를 사용한다.
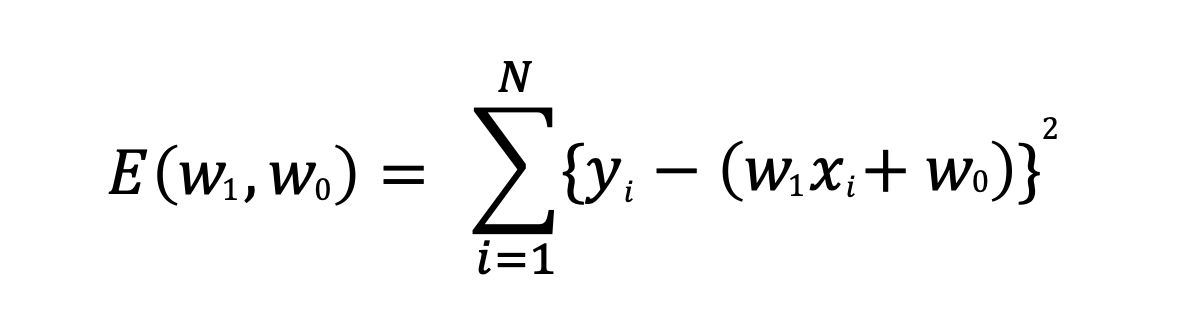
최적의 선형함수(=최소 오차) 구하기
최적의 선형 함수는 최소의 오차를 가지는 선형 함수이며, 이는 곧 앞 섹션에서 정리한 오차함수가 최소의 값(=0)이 되는 w0, w1 값을 구하는 것과 같다.
오차함수가 최소가 되는 w1, w0는 오차함수를 각각 w1과 w0에 대해 편미분을 적용하여 구할 수 있다. 편미분이란, 함수에서 특정 변수에 대한 변화율(미분)을 구하는 과정으로, 이 때 나머지 변수들은 고정된 상수로 간주하는 것이다.
w1에 대한 편미분
w0에 대한 편미분

두 편미분 식을 연립방정식으로
위 두 식의 전체 입력값(xi)의 합과 전체 출력값(yi)의 합은 단순한 계산으로 알 수 있으므로, 이제 이 두 식을 연립방정식으로 풀면 w0와 w1을 구할 수 있다.
예측과 평가
학습 후, 회귀함수의 성능을 평가하기 위해 널리 사용되는 방법 두 가지를 알아보자.
| 평가 방법 | full name | 설명 |
|---|---|---|
| MSE | Mean Squared Error | 평균 제곱 오차. 모든 오차 제곱들의 합. |
| RMSE | Root Mean Squared Error | 평균 제곱근 오차. 모든 오차 제곱들을 합한 뒤, 제곱근을 구한다. 목표 출력값 및 실제값과 같은 단위로 산출되므로, 데이터와의 괴리감을 줄인다. |
(1) MSE
모든 오차의 제곱에 대한 합.
N(테스트 데이터 개수)로 나누는 이유는, 평균을 구하는 것.
(2) RMSE
모든 오차의 제곱에 대한 합의 제곱근.
N(테스트 데이터 개수)로 나누는 이유는, 평균을 구하는 것.
제곱근으로 출력할 경우, 목표 출력값 및 실제값과 같은 단위로 오차가 산출되므로, 데이터와의 괴리감을 줄일 수 있다. MSE의 경우에는 제곱이 들어가기 때문에, 데이터의 단위와 달라 직관적인 평가가 어려울 수도 있다.

Comments